حلّ و ناقش حسب قيم الوسيط الحقيقي
الثلاثي
و إذا كان
نفرض أن
لنحسب
لندرس إشارة
بما أن
منه
و يأخذ إشارة
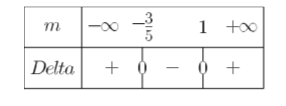
نستنتج مجموعة حلول المعادلة
إذا كان
إذا كان
إذا كان



Les Services iMadrassa sont opérés par la Société HADDAR Consulting au travers du Site internet iMadrassa.com.
Les présentes Conditions Générales d'Abonnement ont pour objet de définir les modalités d'Abonnement et de mise à disposition des Services iMadrassa opérés par la Société HADDAR Consulting, au Souscripteur.
Toute souscription d'Abonnement et toute utilisation des Services iMadrassa implique l'entière acceptation des présentes Conditions Générales d'Abonnement et engage le Souscripteur à les respecter et à les faire respecter par le ou les Élèves qui auront accès au Site internet iMadrassa.com à travers son Abonnement.
Pour un montant défini en fonction de la durée de l'Abonnement choisi par le Souscripteur, la Société HADDAR Consulting fournit des services d'accompagnement scolaire digital.
Parmi ces services, la Société HADDAR Consulting propose quatre outils de suivi :
Le tableau de bord, qui permet de suivre les progrès du ou des Élèves et d'aider à évaluer leurs acquis et leurs lacunes. L'historique des connexions, qui indique les cours étudiés, et les exercices effectués par chaque Élève lors des connexions précédentes ainsi que son temps de connexion. Le score, qui fait un état des points cumulés par chaque Élève.
Préalablement à l'Abonnement aux Services iMadrassa, le Souscripteur devra s'assurer qu'il remplit les conditions nécessaires définies ci-après : Le Souscripteur est responsable de l'utilisation qui peut être faite des Services iMadrassa par les Élèves qui disposeront d'un accès par l'Abonnement du Souscripteur. Le Souscripteur disposant d'un Abonnement peut créer jusqu'à cinq comptes Élève par Abonnement. Pour souscrire aux Services iMadrassa, le Souscripteur doit disposer d'un ordinateur et d'un abonnement à un fournisseur d'accès au réseau Internet. Les frais afférents à ces éléments sont à la charge exclusive du Souscripteur et ne sont pas inclus dans l'Abonnement souscrit auprès de la Société HADDAR Consulting. Pour accéder aux Services iMadrassa, le Souscripteur doit veiller à ce que son équipement informatique dispose d'une configuration compatible à celle requise pour l'utilisation du Site internet iMadrassa.com. Il appartient au Souscripteur de s'assurer de cette compatibilité. La demande d'Abonnement est enregistrée lorsque le Souscripteur a correctement rempli le formulaire d'inscription et réglé le prix de l'Abonnement avec les moyens de paiement qui lui sont proposés et qu'il aura choisis. A réception du paiement, le Souscripteur reçoit immédiatement un courrier électronique, à l'adresse renseignée par lui, qui confirme son Abonnement et dans lequel lui sont délivrés ses identifiants (pseudo et mot de passe).
Les identifiants transmis au Souscripteur sont personnels et confidentiels. L'Utilisateur en est seul responsable et s'engage à ne pas les divulguer. L'accès ultérieur aux Services iMadrassa nécessite l'utilisation de ces identifiants (pseudo et mot de passe).
L'Utilisateur peut modifier à tout moment ses identifiants (pseudo et mot de passe). Cependant, l'Utilisateur s'engage à ne pas utiliser un pseudo à consonance injurieuse, déplacée, discriminatoire, ou contraire au respect de la dignité et de la nature humaine. A défaut, la Société HADDAR Consulting se réserve, à sa seule discrétion, le droit de suspendre l'accès à ce Souscripteur, le temps de l'informer d'une telle incompatibilité et de lui permettre de choisir un pseudo plus approprié, dans les conditions définies à l'article 8.7. des présentes.
Après validation de l'Abonnement, le Souscripteur pourra renseigner les champs le concernant et créer le ou les compte(s) « Élève », dans la limite de cinq comptes par Abonnement au sein d'une famille.
5.1. Fourniture d'informations exactes et identification Le Souscripteur s'engage à communiquer des coordonnées et informations bancaires exactes à la Société HADDAR Consulting qui seront enregistrées lors de sa prise d'Abonnement aux Services iMadrassa. Le Souscripteur s'engage à mettre à jour ses coordonnées au fur et à mesure des éventuels changements de celles-ci, de manière à ce que les informations relatives à chaque Souscripteur à la disposition de la Société HADDAR Consulting soient toujours exactes pendant toute la durée du Contrat liant les parties. La Société HADDAR Consulting ne saurait être tenue responsable au cas où elle n'aurait pas été avisée d'un changement de situation du Souscripteur. En cas de décès du Souscripteur, il appartient aux ayants droits de résilier l'Abonnement dans les conditions définies à l'article 8 des présentes.
5.2. Obligations propres à l'utilisation des Services IMadrassa Le contenu du Site internet iMadrassa.com (fiches de cours, QCM, exercices interactifs, marques, graphismes, vidéos etc.) est protégé par le Code de la Propriété Intellectuelle ainsi que toutes normes internationales applicables, et constitue, sauf indications contraires, la propriété intellectuelle exclusive de la Société HADDAR Consulting. Ce contenu ne peut être consulté par les Utilisateurs qu'à titre personnel, à des seules fins pédagogiques et éducatives, dans le cadre de l'Abonnement contracté par le Souscripteur à cet effet et dans le respect des conditions des présentes.
La Société HADDAR Consulting ne concède aux Utilisateurs aucune licence ni aucun autre droit que celui de consulter le Site internet iMadrassa.com aux fins susvisées. En conséquence, le Souscripteur s'engage, tant en son nom qu'aux noms des Élèves utilisant les Services iMadrassa par le biais de son Abonnement, notamment :
A ne pas diffuser ou divulguer tout ou partie du contenu du Site internet iMadrassa.com par quelque moyen que ce soit ; A ne pas télécharger autrement que dans les cas autorisés par la Société HADDAR Consulting et, plus généralement, à ne pas fixer et reproduire sur tout support quel qu'il soit, par quelque procédé que ce soit tout ou partie du contenu du Site internet iMadrassa.com, à la seule exception d'une impression sur support papier dans les limites ci-après ; En cas d'impression sur support papier de tout ou partie du contenu du Site internet iMadrassa.com, le Souscripteur garantit que toutes les mentions figurant éventuellement sur le contenu ainsi imprimé relatives à la protection des droits seront reproduites sans modifications. Ces copies ne pourront être utilisées que par les seuls Utilisateurs à des fins personnelles pour leur seul usage privé à l'exclusion de tout autre et ne pourront en aucun cas être diffusées ou divulguées auprès des tiers. Plus généralement, à ne pas exploiter et/ou utiliser tout ou partie du contenu du Site internet iMadrassa.com par quelque moyen que ce soit et sous quelque forme que ce soit à des fins autres que celles expressément autorisées. Toute utilisation même partielle du contenu du Site internet iMadrassa.com, ou d'un quelconque de ses éléments, contraire aux présentes engagera la responsabilité du Souscripteur, notamment à l'égard de la Société HADDAR Consulting, et sera susceptible de l'exposer à des sanctions pénales.
En outre, en cas de violation par l'Utilisateur de l'une des présentes conditions, la Société HADDAR Consulting sera habilitée, de plein droit et sans préavis, à suspendre l'accès aux Services iMadrassa et/ou à résilier l'Abonnement du Souscripteur, et conservera à son profit toute somme payée par celui-ci, dans les conditions définies à l'article 8.7. des présentes. En outre, toute somme éventuellement due deviendra immédiatement exigible sans préjudice de tous dommages-intérêts supplémentaires éventuels.
6.1. Fourniture des Services iMadrassa La Société HADDAR Consulting s'engage à fournir un accès aux Services iMadrassa conforme aux normes en vigueur et aux spécifications contractuelles, 24 heures sur 24 et 7 jours sur 7.
A titre exceptionnel, à des fins de maintenance ou de mise à jour, la Société HADDAR Consulting pourra suspendre l'accès à tout ou partie des Services iMadrassa pendant une période consécutive de 24 heures pour des raisons indépendantes de sa volonté ou nécessaires pour assurer la continuité des Services dus au Souscripteur.
En dehors des cas justifiés par l'urgence ou la force majeure, la Société HADDAR Consulting s'engage à prévenir le Souscripteur sur son Site internet iMadrassa.com de toute interruption des Services iMadrassa.
6.2. Obligations de confidentialité - Protection des données à caractère personnel
Les informations nominatives déclarées par le Souscripteur et tout élément d'identification le concernant sont destinés à la Société HADDAR Consulting, qui est autorisée par le Souscripteur à les conserver en mémoire informatique et à les utiliser. Les informations détenues par la Société HADDAR Consulting ne seront pas utilisées à des fins commerciales autres que la commercialisation des Services iMadrassa ainsi que ceux de ses partenaires.
En application de la législation en vigueur, les informations nominatives et tout élément d'identification concernant le Souscripteur pourront être communiqués sur réquisition des autorités judiciaires, ou à une autre société assistant la Société HADDAR Consulting dans la prévention ou la recherche de fraude.
7.1. Responsabilité de la Société HADDAR Consulting La Société HADDAR Consulting est responsable de la bonne exécution de ses obligations contractuelles dans le cadre des normes en vigueur. Toutefois, la responsabilité de la Société HADDAR Consulting ne saurait être engagée si l'inexécution ou la mauvaise exécution du Contrat est imputable, soit au Souscripteur, soit à tout fait imprévisible et insurmontable d'un tiers au Contrat, soit à un cas de force majeure.
7.2. Responsabilité du Souscripteur Le Souscripteur est responsable de la bonne exécution de ses obligations contractuelles dans le cadre de la législation et des normes en vigueur.
7.3. Cas de force majeure ou cas fortuit Ni la Société HADDAR Consulting, ni le Souscripteur ne peuvent pas être tenues pour responsables, ou considérées comme ayant failli au titre de l'Abonnement, pour tout retard ou inexécution, lorsque la cause du retard ou de l'inexécution est liée à un cas de force majeure ou à un cas fortuit habituellement reconnu par la jurisprudence. Pendant toute la durée du cas de force majeure ou du cas fortuit, les obligations nées du Contrat sont suspendues.
7.4. Exonération de responsabilité La Société HADDAR Consulting s'efforce d'assurer au mieux de ses possibilités l'accès permanent aux Services iMadrassa ainsi que la mise à jour des informations figurant sur le Site internet iMadrassa.comdont elle se réserve le droit de corriger, à tout moment et sans préavis, le contenu. La Société HADDAR Consulting tient à signaler que : Les exemples utilisés dans le contenu du Site internet iMadrassa.com ne constituent pas des règles mais ont pour objet l'illustration pédagogique d'une ou plusieurs règles. Certaines rédactions peuvent être transformées par les systèmes d'impression, au point que leur signification devienne erronée. Les opérations de téléchargement peuvent entraîner la disparition d'un bloc de caractères, supprimant ainsi une information essentielle. Le Souscripteur s'interdit, en conséquence, de réclamer quelque indemnisation que ce soit à la Société HADDAR Consulting ou aux Services IMadrassa, pour quelque préjudice que ce soit qui trouverait sa cause dans l'un des cas ou dans l'une des hypothèses précédemment exposés.
La Société HADDAR Consulting propose un type d'Abonnement. Ces un type d'Abonnement, comme tout autre type d'Abonnement que proposerait la Société HADDAR Consulting, donnent à chaque Souscripteur, pendant la durée de validité de l'Abonnement, et sous réserve du respect des obligations de chaque partie, un droit d'accès illimité au contenu désigné dans l’offre.
8.1. Entrée en vigueur L'Abonnement prend effet à compter de la date d’activation du code du Souscripteur. Les modes de paiement proposés peuvent différer selon le type d'Abonnement choisi. Dès réception du paiement, le Souscripteur est averti par courrier électronique ou par SMS, à l'adresse renseignée par lui, de la validation de son Abonnement et de la prise d'effet du Contrat.
8.2. Suspension ou Résiliation de l'Abonnement à l'initiative de la Société HADDAR Consulting La Société HADDAR Consulting pourra suspendre, de plein droit et à sa seule initiative, l'accès aux Services iMadrassa en cas d'utilisation par un Utilisateur d'un identifiant à consonance injurieuse, déplacée ou discriminatoire ou portant atteinte au respect de la dignité et de la nature humaine. Cette suspension sera effective le temps de permettre à l'Utilisateur de choisir un identifiant plus approprié.
La Société HADDAR Consulting pourra suspendre, de plein droit, l'accès aux Services iMadrassa en cas de violation grave ou renouvelée par l'Utilisateur de ses obligations légales ou contractuelles. Une fois la suspension effective et huit jours après la mise en demeure par voie électronique, à l'adresse renseignée par lui, et/ou par lettre recommandée avec demande d'avis de réception restée sans effet, La Société HADDAR Consulting pourra procéder à la résiliation de l'Abonnement sans autres formalités.
En cas de défaut de paiement et de non régularisation et après suspension de l'accès aux Services iMadrassa, la Société HADDAR Consulting procédera sans autre formalité à la résiliation du Contrat après une mise en demeure par voie électronique, à l'adresse renseignée par lui, et/ou lettre recommandée avec demande d'avis de réception restée sans effet pendant huit jours.
Le Souscripteur sera informé de toute modification contractuelle au moins un mois avant son entrée en vigueur par courrier électronique, à l'adresse renseignée par lui, et sur le Site internet iMadrassa.com. En cas de désaccord, le Souscripteur aura la faculté de résilier son Abonnement dans le mois suivant l'entrée en vigueur des modifications, sans droit à dédommagement.
L'utilisation continue des Services iMadrassa pendant un mois à la suite d'une éventuelle modification des présentes Conditions Générales d'Abonnement équivaut à leur acceptation.
Toute notification et autre correspondance devra être adressée à l'adresse suivante :
12 rue Ali Boumendjel
16 000 Alger, Algérie
ou
contact@iMadrassa.com
L'Abonnement de l'Utilisateur et les présentes Conditions Générales d'Abonnement sont régis par le droit algérien.

حلّ و ناقش حسب قيم الوسيط الحقيقي
الثلاثي
و إذا كان
نفرض أن
لنحسب
لندرس إشارة
بما أن
منه
و يأخذ إشارة

نستنتج مجموعة حلول المعادلة
إذا كان
إذا كان
إذا كان
