في كل ما يأتي المستوي منسوب إلى معلم متعامد و متجانس
الجزء الأول
نعتبر الدالة العددية
أدرس اتجاه تغيرات
- لدينا
- دراسة اشارة
لدينا
اما
او
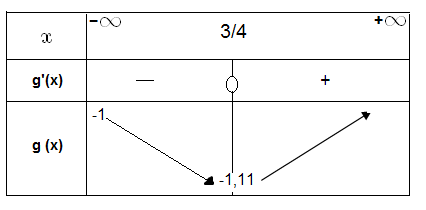
- جدول تغيرات على المجال
أثبت أن النقطة ذات الفاصلة
- لكي تكون الننقطة ذات الفاصلة نقطة انعطاف
يجب ان تنعدم المشتقة الثانية عند القيمة
لدينا
ومنه
اذن النقطة ذات الفاصلة
- لدينا
- ايجاد معادلة المماس لعند النقطة ذات الفاصلة
الشكل العام لمعادلة المماس
ومنه

أثبت أن المعادلة
بما ان
اذن
ومنه المعادلة
استنتج اشارة
لما
لما
الجزء ثاني
أثبت أنه من أجل كل
لدينا
اذن
اذن اشارة
أدرس اتجاه تغيرات الدالة

برّر لماذا الدالتين
المقام دوما موجب على المجال
اشارة المشق للدالة:
الجزء الثالث
نعتبر على المجال
جد احداثيا النقطة
احداثيات النقطة








