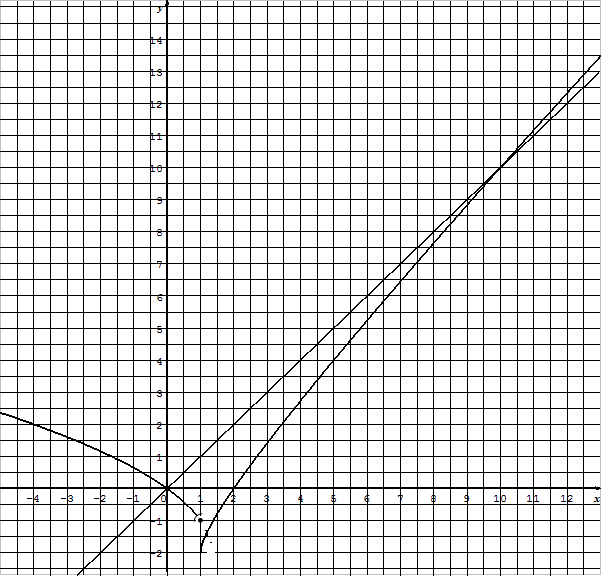
- دالة عددية معرفة بالعبارة :حيثأعداد حقيقيةتمثيلها البياني .
عين
بما أن
وبما أن
إذن :
ولدينا معامل توجيه المماس عند 0 يساوي
لدينا
إذن
إذن :
من (1)
من (2)
وعليه :
ومنه :
وبالتالي
وبالتربيع
إذن :
من (3)
وبالتعويض في (4) نجد :
وعليه
ومنه للمعادلة حلين
ومنه:
و عليه:
- دالة معرفة كما يلي :,تمثيلها البياني .
عين مجموعة تعريف الدالة
ومنه :
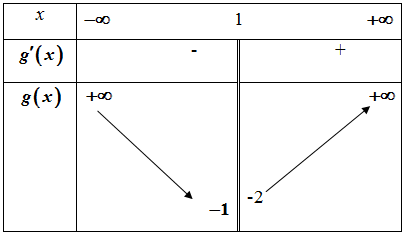
ادرس استمرارية و قابلية الاشتقاق للدالة
- دراسة الاستمرارية عند 1 :
- دراسة الاشتقاق عند 1 :
وعليه
ومنه
ادرس اتجاه تغير الدالة
من أجل
من أجل
ادرس الفروع اللانهائية و المستقيمات المقاربة للمنحنى
هناك فرعين لانهائيين .
لأن :
إذن
لأن :
عين نقط تقاطع
- من أجل :
وعليه
إذن
إذن
ومنه نقط التقاطع هي
- من أجل :
إذن
وعليه :
ومنه
اكتب معادلات المماسات في نقط تقاطع
عند
عند
أنشئ المنحنى