- نعتبر الدالة المعرفة علىبـ :
أحسب نهاية عند
احسب
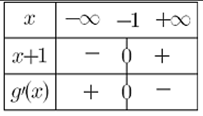
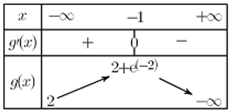
بين أن المعادلة
بماأن الدالة مستمرة و رتيبة تماما (متناقصة تماما) على المجال
وحسب مبرهنة القيم المتوسطة فإن المعادلة تقبل حلا وحيدا
إشارة
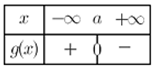
- نعتبر الدالة المعرفة علىكما يلي :نرمز بإلى تمثيلها البياني في معلم متعامد و متجانس(الوحدة)
احسب نهاية
احسب
إشارة
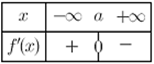
جدول التغيرات :
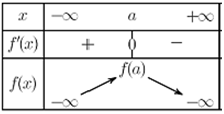
بين أن :
ولدينا أيضا :
حصر
ومن جهة
أي:
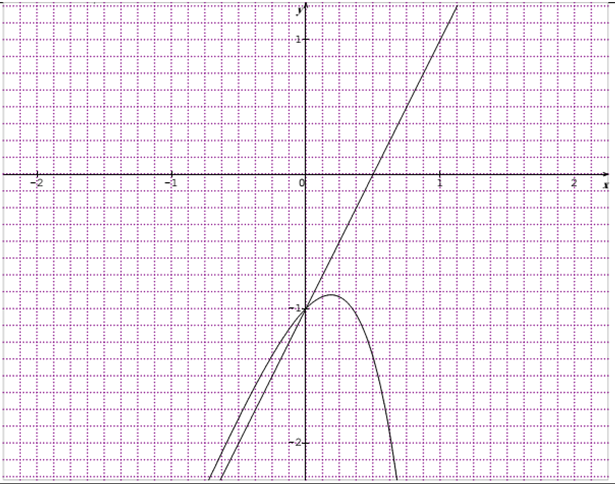
ليكن المستقيم
المستقيم
ادرس وضعية
دراسة الوضعية :
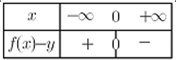
من أجل كل
من أجل كل
نعتبر الدالة
- تحقق أن :
- احسب وتحقق أن :
- استنتج إشارة على
- التحقق أن
بما أن
- حساب المشتقة:
- إشارة :









