نعتبر الدالة
أدرس اتجاه تغير الدالة
لدينا:
دراسة اتجاه تغير الدالة:
لدينا من أجل كل
و بالتالي المنحنى الممثل للدالة
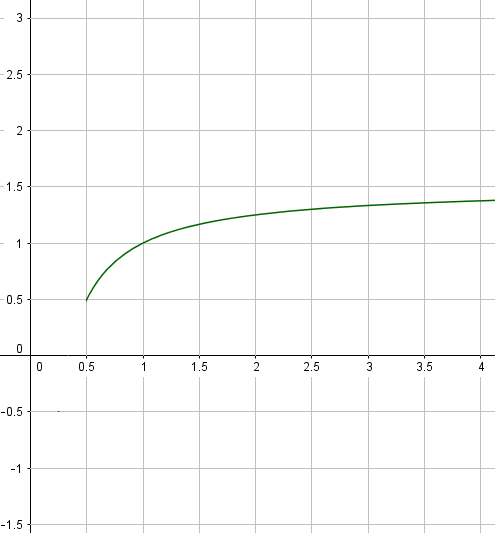
- مثل الحدود و على محور الفواصل مبرزا خطوط الإنشاء
تمثيل الحدود
لتمثيل الحدود على محور الفواصل نستعمل المنحنى
- برهن بالتراجع أنه من أجل كل عدد طبيعي :
البرهان بالتراجع أنه من أجل
- من أجل لديناو منه
- نفرض أن و نبين أن.
لدينا
إذن من أجل كل عدد طبيعي
- بين أن المتتالية متناقصة تماما. ماذا تستنتج؟
بيان أن
الطريقة الأولى:
لدينا:
وبما أن
و منه فالمتتالية
الطريقة الثانية: نبرهن بالتراجع أنه من أجل كل
- من أجل لدينا:وو منه
- نفرض أن و نبين أن.
لدينا
و بالتالي
- الإستنتاج: بما أن المتتالية متناقصة تماما و محدودة من الأسفل بالعددفإنمتقاربة.
- أثبت أنه من أجل كل عدد طبيعي:
إثبات أنه من أجل كل عدد طبيعي
لدينا من جهة:
و من جهة أخرى لدينا:
- بين أنه من أجل كل عدد طبيعي :، ثم استنتج نهاية المتتالية
بيان أنه من أجل كل عدد طبيعي
لدينا:
بضرب أطراف المتباينات طرفا لطرف و بعد اختزال العوامل المتساوية نجد:
لدينا
لتكن
- بين أن هندسية يطلب تعيين أساسها و حدها الأول ثم أكتب عبارةبدلالة.
بيان أن المتتالية
لدينا:
أساسها
إذن:
- أحسب المجموع حيث:
حساب المجموع
لدينا:
و منه
و منه








