الجزء الأول : قراءة بيانية
ليكن في المستوي المنسوب إلى معلم ، المنحنيين (C)و(P)الممثلين لدالتين معرفتين و قابلتين للاشتقاق على
نعلم أن إحدى هاتين الدالتين هي مشتقة الدالة الأخرى . نرمز بـ
اعتمادا على الشكل المقابل ، الذي يعطي التمثيلين البيانيين للدالتين
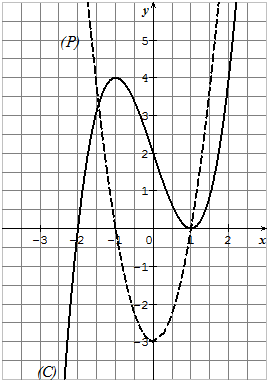
أرفق بكل من الدالتين
حيث
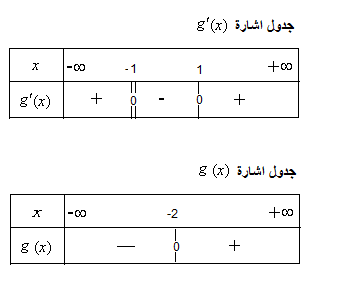
جدول تغيرات كل الدالة


ما هو معامل توجيه المماس للمنحنى (C)عند النقطة ذات الفاصلة 0 ؟
معامل توحيد المماس للمنحنى (C) عند النقطة ذات الفاصلة 0 هو -2
الجزء الثاني : دراسة دالة
لتكن الدالة المعرفة على
نرمز بـ
عين الدالة المشتقة
لدينا :
إشارة
لدينا :
ومنه
إذن
جدول تغيرات f على المجال

استنتج حصرا لـ
لما
عين معادلة لـ
لدينا : الشكل العام لمعادل المماس
بما أن
إذن معادلة المماس هي :
عين قيمة مقربة لـ








