- الجدول التالي هو جدول تغيرات الدالة العددية و المعرفة على المجالكمايلي:
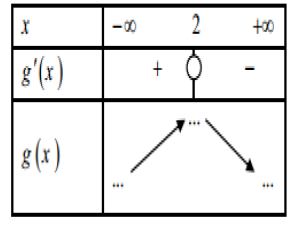
أحسب
حساب
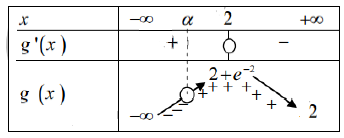
علل وجود عدد حقيقي وحيد
يحقق
تعليل وجود عدد حقيقي
الدالة
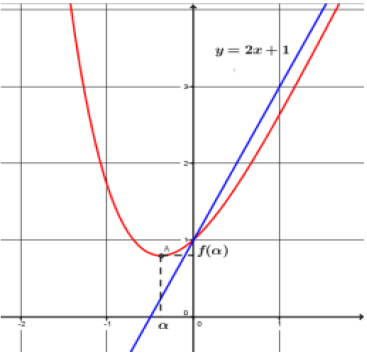
ومنه حسب المبرهنة القيم المتوسطة يوجد عدد حقيقي وحيد
إستنتج إشارة
إستنتاج إشارة
مما سبق نجد أن إشارة

- الدالة العددية المعرفة على المجالب:
و
بين أن :
حساب النهايات :
- بين أنه من أجل كل من:ثم إستنتج إشارةثم شكل جدول تغيرات الدالة.
- بين أن:
،ثم جد حصرا للعدد.
نبين أن من أجل كل
لدينا الدالة
ومنه إشارة
جدول تغيرات الدالة
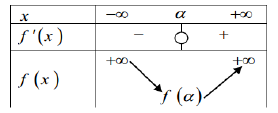
تبيان أن
لدينا ،
تعيين الحصر : لدينا
من جهة أخرى ،
إذن :
بين أن المنحنى
تبيان
لدينا،
- بين أن يقبل مستقيما مائلامعادلته:بجوار.
- أدرس وضعية بالنسبة للمستقيم.
- أنشئ المنحنى في المعلم السابق وعلى المجال(تعطى)
- تبيان أن يقبل مقاربا مائلا :
لدينا ،
- دراسة الوضعية : ندرس إشارة الفرق :
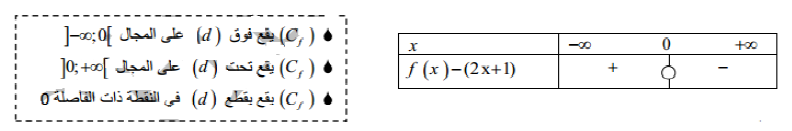
ناقش قيم الوسيط الحقيقي
حلول المعادلة
المناقشة :
لتكن الدالة
بالستعمال مشتق دالة مركبة،إستنتج إتجاه تغير الدالة
تعيين إتجاه الدالة
إشارة
حسب السؤال 2 ) نجد :

حساب النهايات :
- لأن
-
لأن









