- لتكن الدالة المعرفة علىكما يلي :
عين قيمتي العددين الحقيقين
تعيين قيمتي
لدينا :
إذن :
- نعتبر الدالة المعرفة علىكمايلي :،
وليكن
أثبت أنه من أجل كل
إثبات أن :
إذن :
- أدرس تغيرات الدالة
- أثبت أن المنحنى يقبل مستقيمين مقاربينومعادلتهاوبجواروعلى الترتيب .
- أدرس الوضع النسبي للمنحنى بالنسبة إلى من المستقيمين و.
- دراسة تغيرات الدالة
الدالة المشتقة:
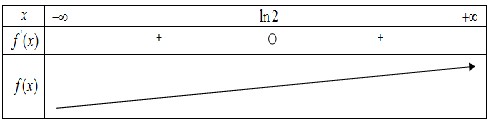
جدول التغيرات :
- بيان أن يقبل مستقيمين مقاربين مائلينو
- دراسة الوضع النسبي ل بالنسبة لو
بين أن المنحنى
بيان أن
بماأن
أثبت أن المعادلة
بيان أن المعادلة
ومنه حسب مبرهنة القيم المتوسطة فالمعادلة
أنشئ المستقيمين
إنشاء
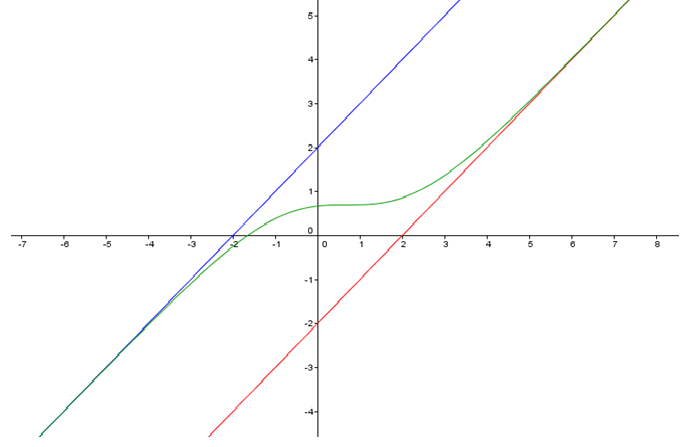
ناقش بيانيا حسب قيم الوسيط الحقيقي m عدد وإشارة حلول المعادلة :
المناقشة البيانية
- إذا كان أوفإن المعادلة لاتقبل حلولا .
- إذا كان فإن المعادلة تقبل حلا وحيدا موجبا تماما
- إذا كان فإن المعادلة تقبل حلا معدوما
- إذا كان فإن المعادلة تقبل حلا وحيدا سالبا تماما








