لتكن
نعتبر المعادلة التفاضلية
حل المعادلة التفاضلية
حل المعادلة التفاضلية :
لدينا :
وبالتالي فإن حلول المعادلة التفاضلية
استنتج أن الدالة
استنتاج أن الدالة
الدالة
الدالة
تحقق أن الدالة
التحقق أن الدالة
الدالة
بملاحظة أن
بيان أن الدالة
لدينا :
ومنه:
نستنتج أن
نسمى
أثبت أنه من أجل كل
إثبات أنه من أجل كل
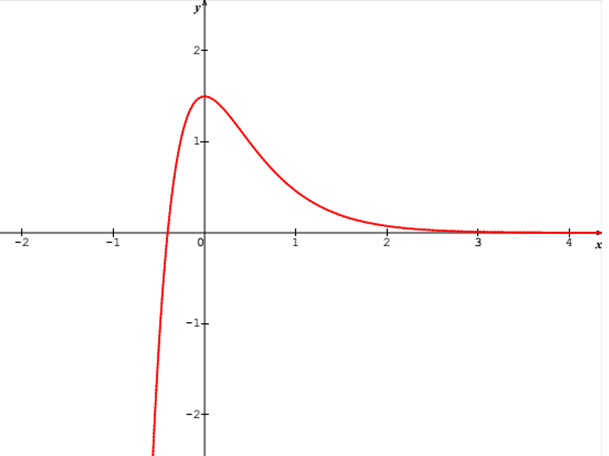
عين نهاية
حساب نهايات الدالة
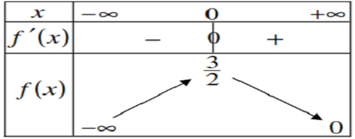
ادرس اتجاه تغير الدالة
دراسة اتجاه تغيرالدالة
لدينا:
إشارة
عين نقط تقاطع المنحنى
تعيين نقط التقاطع مع المحاور:
- مع محور الفواصل:
و منه
- مع محور التراتيب:
احسب
حساب