التمرين 04
-
أثبت أن :
إذا كانمثلث حيثفإن مساحة المثلثهيحيث :
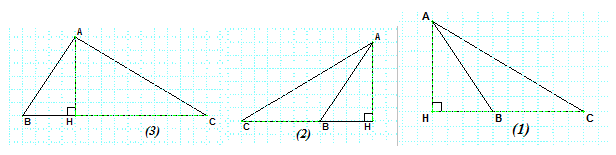
نغلم أن مساحة المثلث
تساوي
في كل الحالات
و منه
منه مساحة المثلث
تساوي
و بتغير تسمية النقط نجد العبارات الأخرى للمساحة
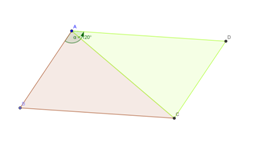
- احسب مساحة المتوازي الاضلاع
علما أن:
و
و
لنحسب $$S^{'}$$ مساحة المثلث $$ABC$$ علما أن $$\hat{B} = 60° = \frac{\pi}{3}$$ وأن $$(AB = 3cm)$$ و $$(BC = AD = 5cm)$$
$$S^{'} = \frac{1}{2} ac.sin\hat{B} = \frac{1}{2} \times BC \times AB \times sin\hat{B}$$ و منه $$S^{'} = \frac{1}{2} \times 5 \times 3 \times sin(\frac{\pi}{3})$$
$$S^{'} = \frac{15}{2} \times \frac{\sqrt{3}}{2} = \frac{15\sqrt{3}}{4}cm^2$$ و منه مساحة المتوازي الاضلاع $$ABCD$$ هي $$S = 2S^{'}$$
و هي $$S = 2 \times \frac{15\sqrt{3}}{4} cm^2$$ و هي $$S= \frac{15\sqrt{3}}{2} cm^2$$
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
