- دالة معرفة على المجالكمايلي :
باستعمال
من أجل
احسب
بين أن الدالة
ومنه
ادرس اتجاه تغير الدالة
لدينا
الدالة متناقصة على المجال
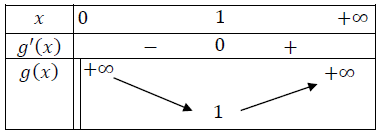
استنتج أنه من أجل كل عدد حقيقي
حسب جدول تغيرات
- نعرف الدالة على المجالكما يلي :وليكن تمثيلها البياني في المستوي المنسوب إلى معلم متعامد و متجانس
احسب
بين أنه من أجل كل
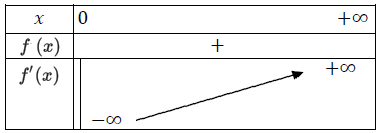
منه الدالة المشتقة للدالة
استنتج اتجاه تغير الدالة
الدالة متزايدة تماما على المجال
بين أن
ومنه المستقيم
حامل محور التراتيب مقارب ثاني
نعتبر الدالة
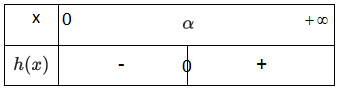
- بين أن المعادلة تقبل حلا وحيدامن المجال
بما أن الدالة
- ادرس الوضع النسبي للمنحني و المستقيم.
نلاحظ أن
من أجل كل
و من أجل كل
ارسم








