- الجزء الأول :
نعتبر الدالة
و نرمز بـ
أحسب نهاية الدالة
حساب نهاية الدالة
ومنه :
نستنتج بالنسبة للمنحنى
أحسب
حساب
من أجل كل
ومنه فإن الدالة
أكتب معادلة للمماس
كتابة معادلة المماس
معادلته:
- بين أن المعادلة : تقبل حلا وحيدا
- بين أن ينتمي إلى المجالثم عين حصرا للعددسعته؟
نبين أن المعادلة
الدالة
ومنه ينتج:
إذن المعادلة
ينتج أن :
و كون
نستنتج أن
باستعمال الآلة الحاسبة نجد أن :
و منه
و بالتالي ينتج حصرا للعدد
أي :
أرسم
رسم المنحنى
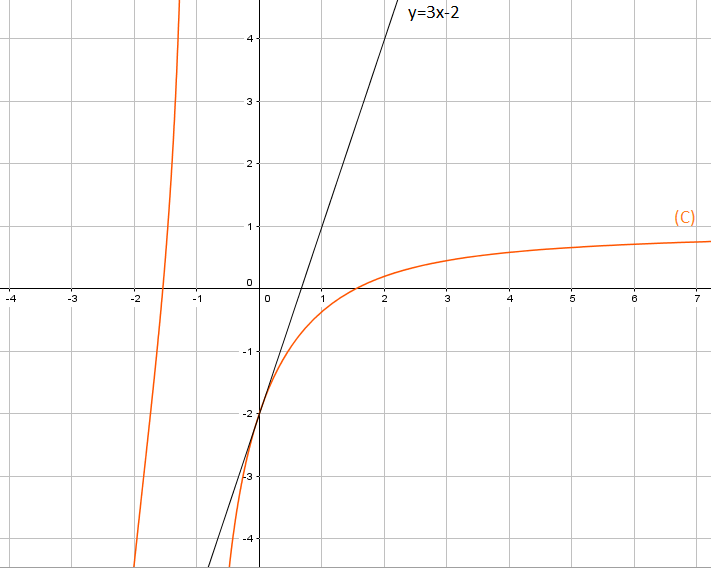
- عين العددين الحقيقين وحيث من أجل كل:
ومنه
- استنتج بـ مساحة حيز للمستوي المحدد بـ :وو المستقيم ذو المعادلة
(تقبل أن
نقبل أن
- الجزء الثــــاني :
أحسب
الدالة
من أجل كل
كون
الدالة
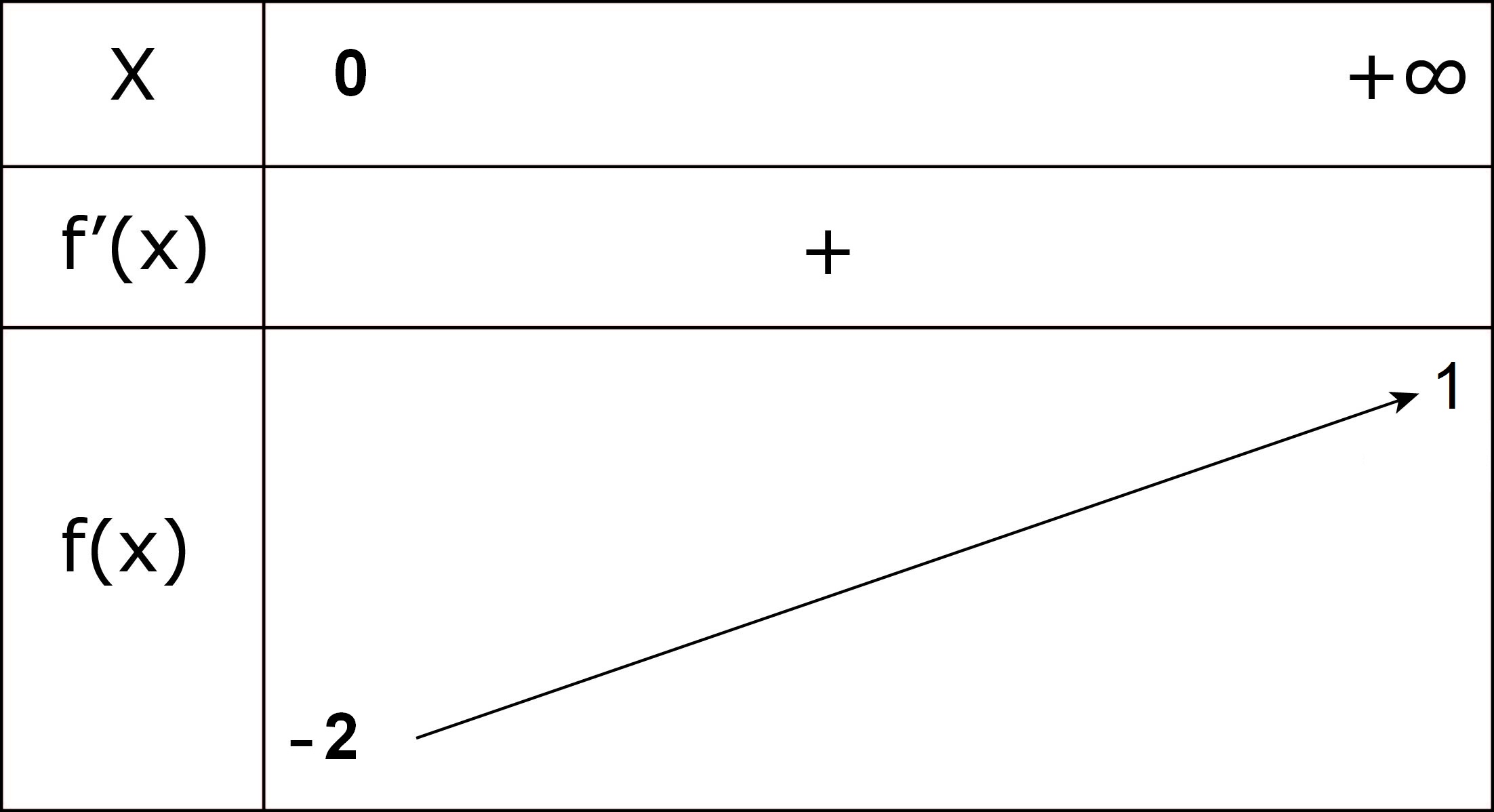
- أحسب ، ما هي إشارتها؟
حساب
من اجل كل
- برهن بالتراجع أنه من أجل كل عدد طبيعي :,ثم استنتج إشارة
نبرهن بالتراجع أن من أجل كل
من أجل
نفرض أن:
من
ومنه
لدينا
فنجد:
أي:
من
نقارن بين
لدينا :
ومنه نستنتج ان
و من
أي:
إذن من أجل كل
لدينا:
نستنتج إشارة :
مما سبق لدينا:
أي أن :
إذن إشارة
- بين أن المعادلة تقبل حلا وحيدا على المجال، نرمز لهذا الحل بـ:
نبين أن المعادلة
الدالة
لدينا :
ومنه ينتج أن :
نستنتج أن المعادلة
أحسب
حساب
من السؤال السابق لدينا:
كون:
نستنتج أن:
أي:
بملاحظة أنه من أجل كل
- بين أن القيمة المتوسطة تساوي لـعلىتساوي:
بملاحظة أنه يوجد من أجل كل
نبين أن القيمة المتوسطة
ومنه:
لدينا:
ليكن:
- استنتج
إستنتاج :
ومنه :
إذن نستنتج أن :








