دالة عددية معرّفة بـ:
بين أن مجموعة تعريف الدالة
مجموعة التعريف:
بالإتحاد :
أدرس إستمرارية الدالة
دراسة الإستمرارية عند
فإن
استنتج أن الدالة
بما أن
علما ان من أجل كل عدد حقيقي من المجال
- استنتج أن المستقيم الذي معادلتهمقارب مائل للمنحنىفي جوار
علما
منه
أدرس تغيرات الدالة
نهايات:
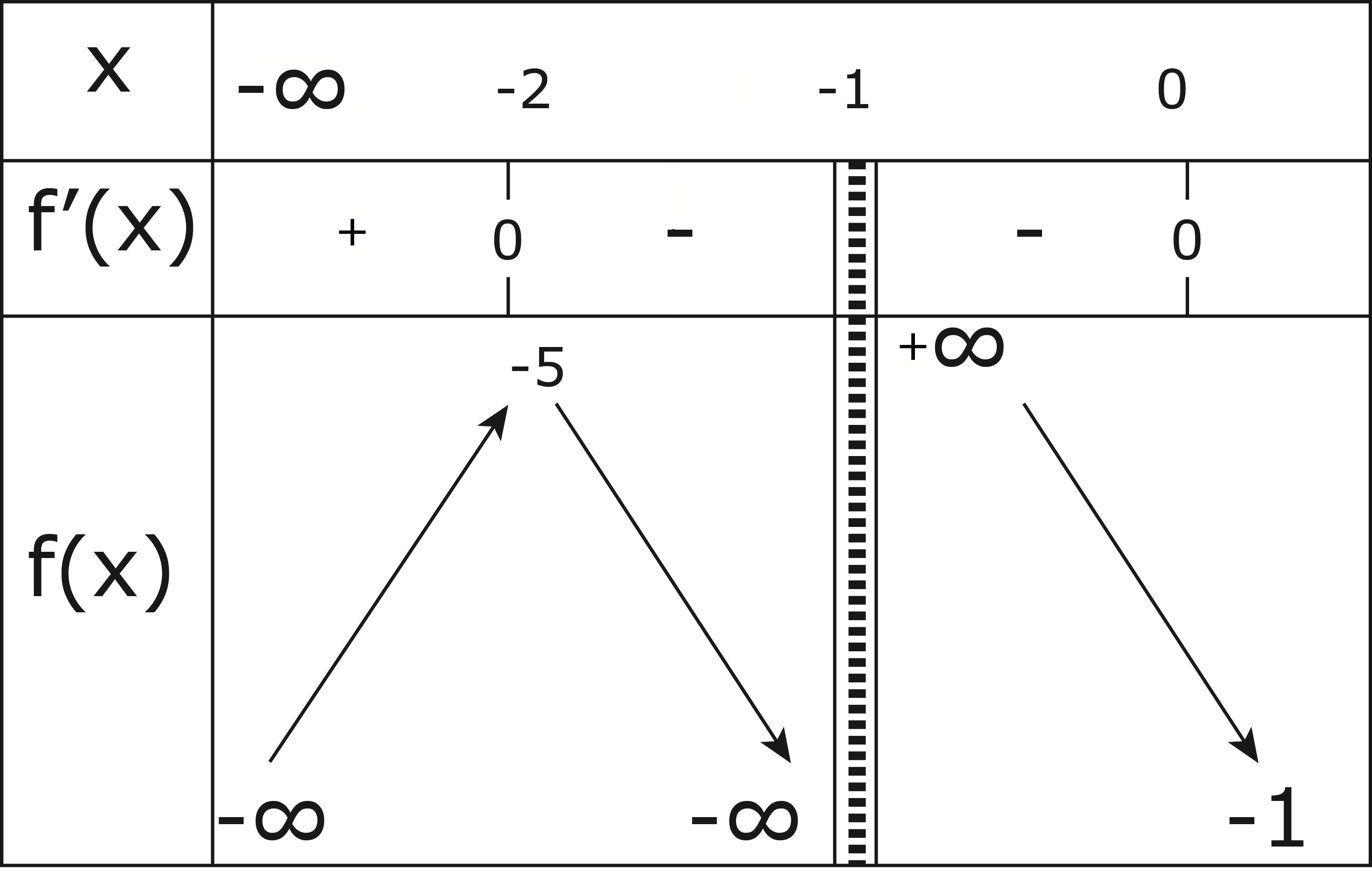
بين أن المعادلة
حسب مبرهنة القيم المتوسطية
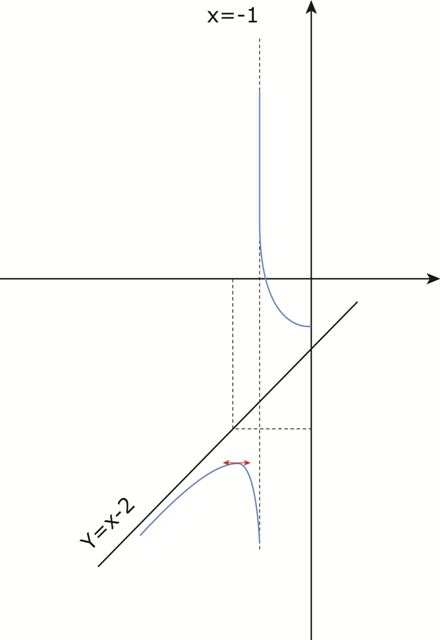
أرسم
رسم
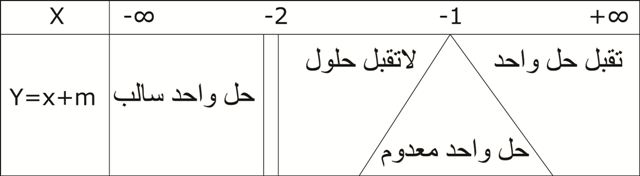
حل المعادلة
حلول المعادلة