لتكن الدالة
- احسب النهايات عند وو
- أدرس تغيرات الدالة و شكل جدول تغيراتها؟
إشارة المشتق : من أجل كل
إذن ندرس إشارة البسط:
إما
جدول التغيرات:
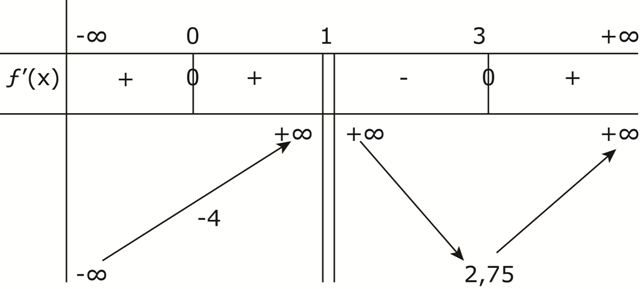
عين الأعداد
بالمطابة مع
منه
بين أن المعادلة
إثبات أن المعادلة
من جدول تغيرات الدالة
إذن :
حسب نظرية المتوسطية فإن:
المعادلة
لدينا:
أنشئ
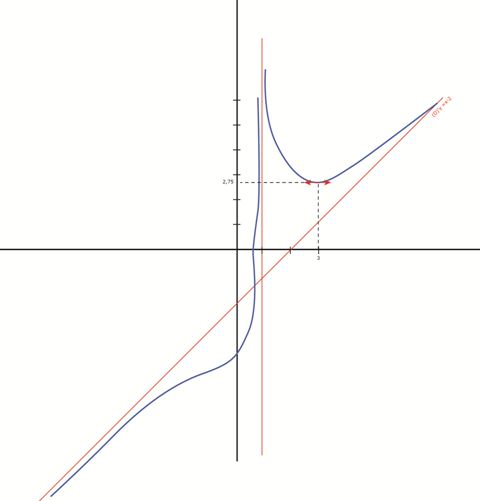
استنتج بيانيا و حسب قيم الوسيط الحقيقي








