نعتبر الدالة
ليكن
- أدرس تغيرات ؟
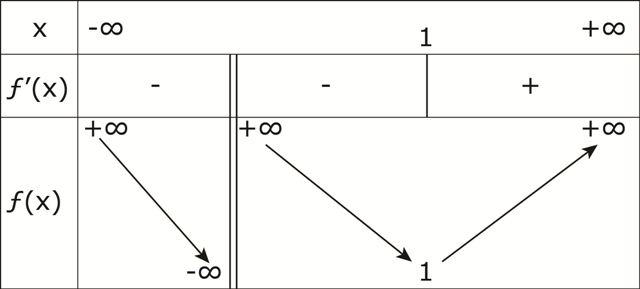
دراسة تغيرات
- تحديد مجموعة التعريف للدالة و لتكن
- حساب النهايات:
من أجل
إشارة
ومنه جدول تغيرات
- بين أن المعادلة تقبل حلا وحيدامنو أن
نبين أن المعادلة
- نلاحظ أن المعادلة لا تقبل أي حلا فيلأن :من أجلمن
إذن
وبما أن
فإن:
- بين أن المنحنى يقبل نقطة إنعطاف؟
نقطة إنعطاف: الدالة
إشارة
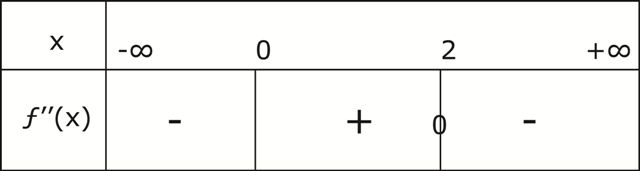
الدالة
إذن للمنحنى نقطة إنعطاف
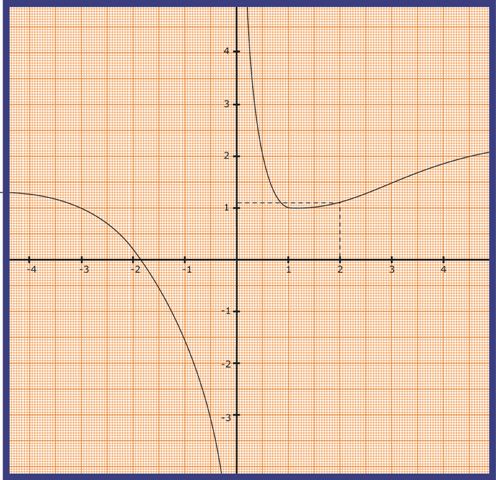
- أدرس الفروع اللانهائية للمنحنى؟
دراسة الفروع اللانهائية :
إذن المنحنى
لدينا:
المنحنى
فالمنحنى يقبل فرعا مكافئا إتجاهه حامل محور السينات
- أنشئ المنحنى؟