جزء 1 : لتكن الدالة
بقراءة بيانية :
عيّن نهايتي الدالة
عيّن
عيّن اتجاه تغيّر الدالة
الدالة
و متزايدة تماما على
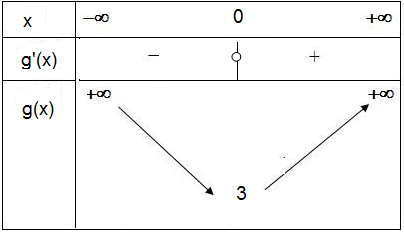
عيّن إشارة الدالة
من أجل كل
عيّن
- باستعمال معطيات سابقة بين أن : .
لدينا :
و لدينا :
و منه :
- احسب نهايات الدالة عند أطراف مجموعة التعريف .
- عيّن اتجاه تغيّر الدالة ثم شكل جدول التغيرات .
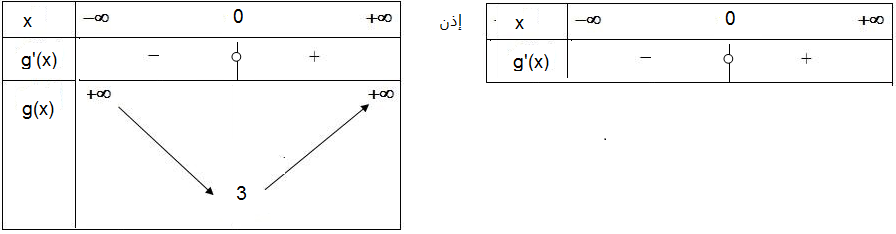
جزء 2 :
بيّن أنه من أجل كل عدد حقيقي
أدرس تغيرات الدالة
حساب النهايات :
المشتقة :
و بما أن
إذن الدالة
جدول التغيرات
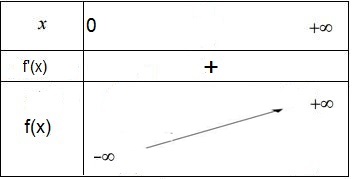
بين أن المعادلة
بما أن الدالة
- أثبت أن المستقيم ذي المعادلةمستقيم مقارب مائل بجوار.
إذن :
- أدرس الوضعية النسبية ل بالنسبة إلى.
لدينا :
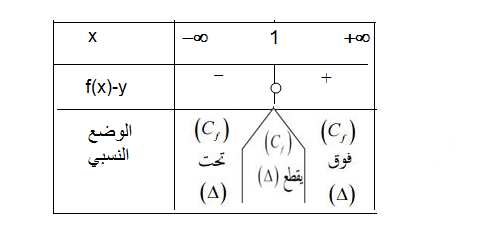
- بيّن أن يقبل نقطة انعطافيطلب تعيين احداثياتها .
إذن : إشارة
بما أن
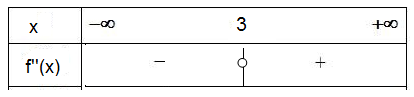
- تحقق أن : هي معادلة المماسلعند النقطة.
لدينا :
إذن
أرسم
- باستخدام و المستقيممثل الحدود،وعلى حامل محور الفواصل .
- بيّن أنه من أجل كل عدد طبيعي فإن :.
من أجل
نفرض أن
لدينا :
و منه : من أجل كل
- بيّن أن المتتالية متناقصة تماما .
بما أن
- ماذا تستنتج ثم عيّن .








