الجزء الأول
لتكن
ليكن
أحسب نهايات الدالة عند
.
بين أن المستقيم
لدينا:
إذن المستقيم
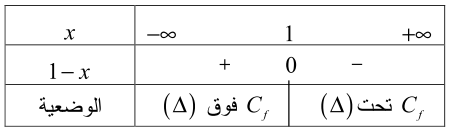
لدراسة وضعية
لدينا:
لتكن
أدرس تغيرات الدالة
لدينا
الدالة
إشارة
نلاحظ أن المعادلة
الدالة
إذن المعادلة
وبالإضافة إلى ذلك لدينا:
وهكذا فإن المعادلة
نستنتج هكذا إشارة
أدرس اتجاه تغير الدالة
الدالة
إذن
بما أن
وهكذا نجد أن
.
احسب
نستنتج هكذا أنه من أجل كل
أنشئ المنحنى
الجزء الثاني :
لتكن
برر وجود الدالة
بما أن الدالة
أدرس اتجاه تغير الدالة
من أجل كل








