نعتبر الدالة
- تحقق أنه من أجل كل عدد حقيقي من:
اذن:
- أحسب نهايات الدالة عند أطراف مجموعة تعريفها.
أدرس اتجاه تغير الدالة
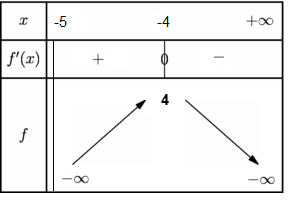
- جدول التغيرات:
بين أن المعادلة
و
و
اذن نستنتج أن المعادلة
حيث
بين ان المنحنى
لدينا :
اذن
ومنه
معادلة المماس
اذن:
أحسب
| 0 | 1 | 3 | 4 |
| ln 5 | -1+ln6 | -3+ln8 | -4+ln9 |
- باستعمال المكاملة بالتجزئة ، أحسب
نضع
ادن :
- احسب مساحة الحيز المستوي المحدد بالمنحنى ومحور الفواصل و المستقيمين ذوا المعادلتين:و








