الجزء الأول :
نعتبر الدالة
- أدرس تغيرات الدالة
- حساب النهايات :
- اتجاه تغير الدالة :
لنعين إشارة
لما
لما :
ومنه الدالة
- جدول التغيرات :
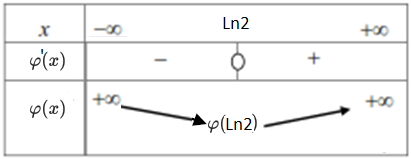
- استنتج حسب قيم العدد الحقيقي ، إشارة
لدينا
بما أن
الجزء الثاني :
نعتبر الدالة
تحقق من أن الدالة
الدالة
أحسب نهاية الدالة
نعتبر الدالة
- أدرس تغيرات الدالة و أحسبو
- حساب النهايات :
- اتجاه تغير الدالة :
إن إشارة
و عليه لما
لما
- جدول التغيرات :
إن
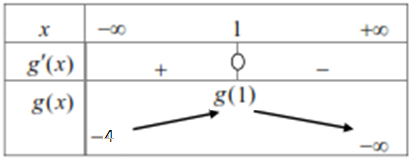
- بين أن المعادلة تقبل حلا وحيدامن المجال
الدالة
مبرهنة القيم المتوسطة المعادلة
- استنتج حسب قيم العدد الحقيقي ، إشارة
اعتمادا على تغيرات الدالة
لما
- بين أنه من أجل كل عدد حقيقي :ثم عين إشارة
إشارة
لما
لما
- أنجز جدول تغيرات الدالة
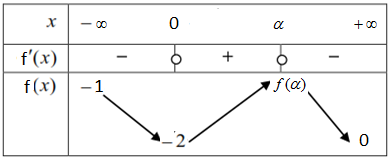
بين أن :
لدينا :
و بالتالي
و عليه
تعيين حصرا ل
لدينا
إذن
عين معادلة المماس
معادلة المماس
أدرس الوضع النسبي للمنحني
لنعين إشارة
لأن من أجل كل

أرسم المماس
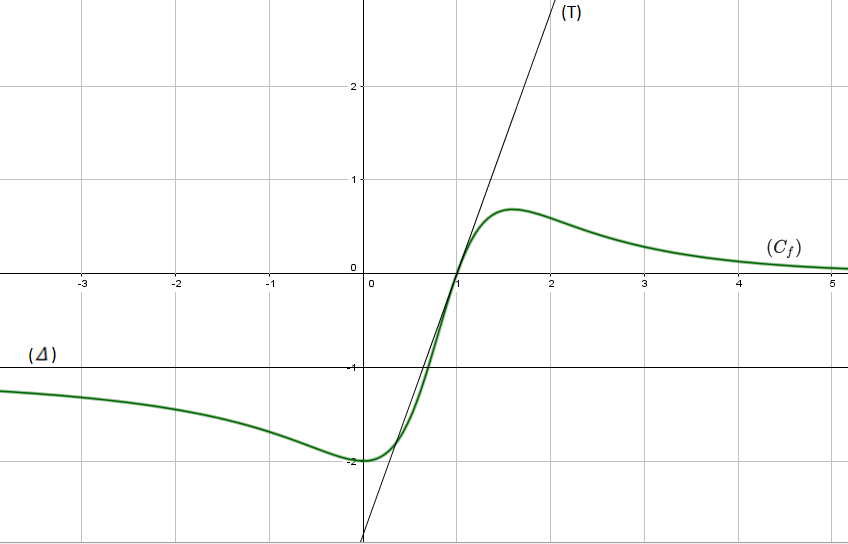
نعتبر الدالة المعرفة على بــ :
- أكتب دون رمز القيمة المطلقة
لما
لما
- أرسم في معلم آخر المنحني موضحا كيفية الرسم
في المجال
في المجال

- عين قيم العدد الحقيقي التي من أجلها تقبل المعادلةثلاث حلول موجبة
المعادلة
و عليه : إذا كان








