ادرس اتجاه تغير الدالة
احسب
لدينا
فإن لما
احسب
- احسب
-
بين أن المستقيم
الذي معادلتهمستقيم مقارب للمنحني
بما أن
- أدرس الوضع النسبي للمنحني و المستقيم
لدينا من أجل كل
لما
لما
لما
- بين أنه من أجل كل من المجال:
الدالة
- ادرس اتجاه تغير الدالة ثم أنجز جدول تغيراتها
إشارة
لما
لما
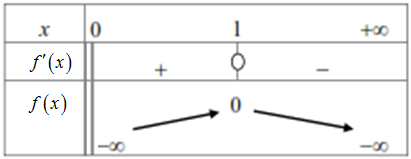
جدول التغيرات :
أرسم المستقيم
- عين الدالة الأصلية للدالةعلى المجالو التي تنعدم عند القيمة
من أجل كل
الدالة
الدالة
و عليه الدوال الأصلية للدالة
مع
و بما أن
- استنتج المساحة ، مساحة الحيز المستوي المحدد بالمنحنيو المستقيمات التي معادلتها;;
لدينا
و عليه








