نعتبر الدالة
نسمي
أحسب
لإن
و عليه
أحسب
إشارة

عين إحداثيات نقط انعطاف المنحني
إن
إشارة
مميز
تعطى إشارة
و بالتالي للمنحنى
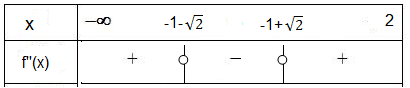
أثبت أن للمنحني
إذا كان
بما أن
و عليه :
و منه :
إذن :
نجد :
و بالتالي :
و منه
معادلة المماس
معادلة المماس
أرسم المماسين
عين بيانيا و ذلك حسب قيم الوسيط الحقيقي
إذن حول المعادلة هي فواصل نقط تقاطع
لما
لما
لما
لما
لما
لما
لما
لما
نعتبر الدالة
- عين ،وبحيث تكون الدالةدالة أصلية للدالةعلى المجال
الدالة
و منه
(لأن :
و عليه
- أحسب مساحةالحيز المستوي المحدد بالمنحنيو المستقيمات التي معادلتها:وومععدد حقيقي من المجال
و عليه :
- احسب








