نعتبر في مجموعة الأعداد المركبة
- بين أن المعادلة تقبل حلان تخيليان صرفان يطلب تعيينهما
نضع
و منه
إذن
و عليه
- عين كثير الحدود بحيث من أجل كل عدد مركب:
لدينا :
و منه :
إذن :
وعليه
وبالتالي :
- عين في المجموعة حلول المعادلة
وعليه
أو
إن:
لنعين حلول المعادلة
مميز هذه المعادلة هو :
الحلين هما :
المستوي منسوب إلى المعلم المتعامد و المتجانس
نعتبر النقط
- أنشئ النقط ،،و
إنشاء النقط
لدينا :
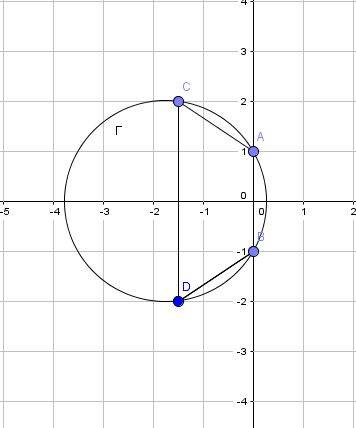
- بين أن النقط ،،وتنتمي إلى الدائرةالتي قطرها
بما أن
إذن
و عليه
من جهة أخرى:
- بين أنه يوجد دوران مركزه المبدأيحول النقطةإلى، يطلب تعيين قيسا بالدرجة لزاوية هذا الدوران (تدور النتيجة إلى الوحدة)
بما أن
و منه
و عليه
عين الشكل الجبري و الشكل الأسي للعدد المركب
لدينا
إن
الإستنتاج : لدينا
و منه








