- نعتبر الدالة المعرفة بالعبارة :
عين
حلول المعادلة :
تعيين الأعداد a و b وc :
ومنه :
وعليه :
وعليه :
ادرس تغيرات الدالة
إشارة المشتق :
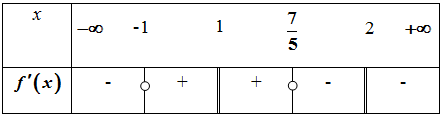
إذن
ومتناقصة تماما على كل من المجالات
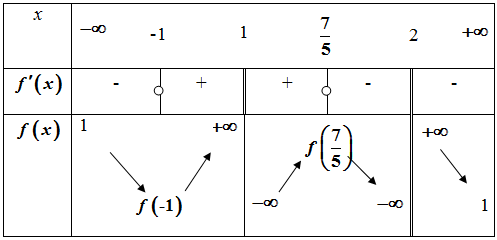
- عين بواسطة معادلاتها المستقيمات المقاربة للمنحنى الممثل لتغيرات الدالة.
بما أن :
وبما أن
- ادرس الوضعية النسبية للمنحنى و المستقيم المقارب الأفقي.
دراسة الوضعية للمنحنى
وعليه
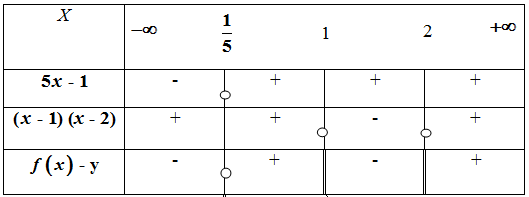
عين تقريب تآلفي للدالة
لنكتب معادلة المماس عند0 :
حيث
وعليه أحسب تقريب تآلفي للدالة
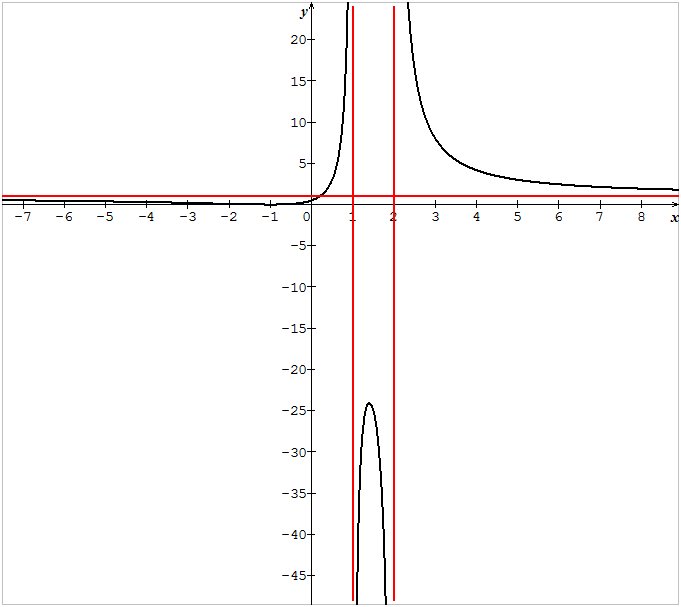
أنشئ
- نعرف الدالة كما يلي :
عين مجموعة تعريف الدالة
نحل المعادلة :
نضع :
و بالتالي :
اكتب
ادرس استمرارية و قابلية الاشتقاق للدالة
- دراسة الاستمرارية عند 0 :
إذن
- قابلية الاشتقاق عند 0 :
إذن
إذن
ادرس شفعية الدالة
لدينا من أجل كل
ولدينا :
ومنه
استنتج التمثيل البياني
لدينا من أجل :
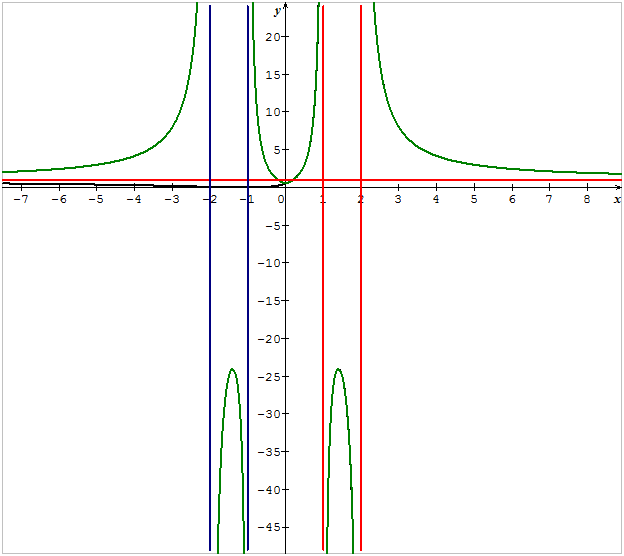
ناقش بيانيا وجود وعدد حلول المعادلة
وعليه :
لما :
لما
لما
لما
لما
لما








