نعتبر الدالة
أدرس تغيرات الدالة
دراسة تغيرات الدالة
- حساب النهايات:
- حساب المشتقة :
من أجل كل
بما أن
- جدول التغيرات :
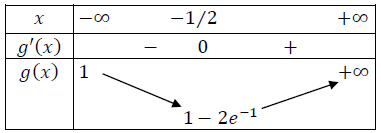
استنتج إشارة
استنتاج إشارة
بما أن
لتكن الدالة
أحسب
حساب النهايات :
أدرس اتجاه تغير الدالة
دراسة اتجاه تغير الدالة
من أجل كل
جدول التغيرات:
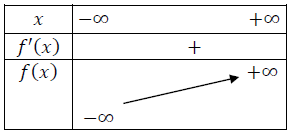
- بين أن المستقيم ذو المعادلةمقارب مائل للمنحنىبجوار
- أدرس الوضع النسبي للمنحنى و المستقيم
- بيان أن مستقيم مقارب مائل للمنحنىبجوار :
لدينا :
-
دراسة وضعية
بالنسبة إلى:لدينا :
ومنه إشارة الفرقمن إشارة
إذا كان
إذا كان
إذا كان
أكتب معادلة المماس
كتابة معادلة المماس عند النقطة
بين أن المنحنى
بيان أن
من أجل كل
أنشئ المستقيمين
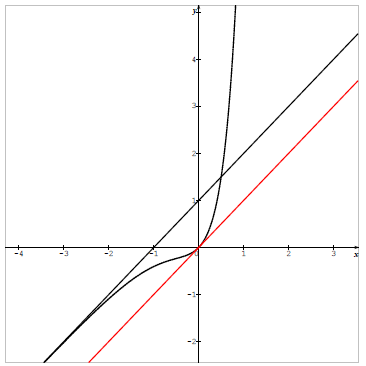
ناقش بيانيا حسب قيم الوسيط الحقيقي
المناقشة البيانية :
لدينا:
بإضافة
أي
إذا كان
إذا كان
إذا كان
إذا كان








