الجزء الأول :
لتكن الدالة
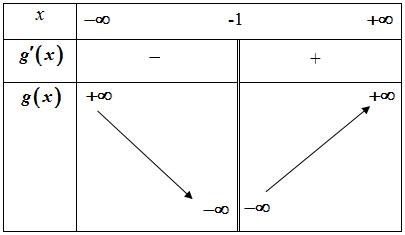
أدرس تغيرات الدالة
لدينا :
و لدينا :
من أجل كل
و منه إشارة
أحسب
حساب
لدينا
استنتاج إشارة
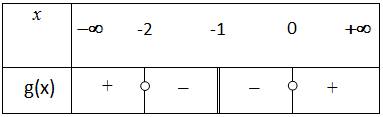
الجزء الثاني:
نعتبر الدالة
- أحسب نهايات الدالة ثم فسر النتائج بيانيا.
و منه :
- أثبت أنه من أجل كل من:.
استنتج اتجاه تغير الدالة
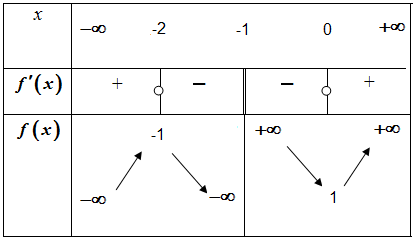
- بين أن المنحنى يقبل مستقيما مقاربا مائلامعادلته.
إذن
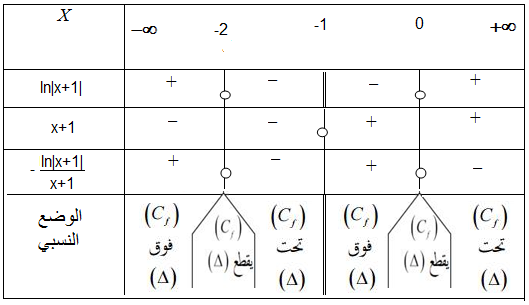
- أدرس وضعية المنحنى $$(C_f)$$ بالنسبة إلى المستقيم $$(\Delta)$$ .
لدينا : $$f(x)-y=-\frac{ln|x+1|}{x+1}$$ و منه الوضع النسبي ل $$(C_f)$$ و $$(\Delta)$$ يتعلق بدراسة إشارة $$-\frac{ln|x+1|}{x+1}$$ .
$$-\frac{ln|x+1|}{x+1}=0$$ يكافئ $${ln|x+1|}=0$$ و منه :$$|x+1|=1$$
إذن : $$\begin{cases} x+1=1 \\وأ \\-x-1=1 \end{cases} $$ إذن : $$\begin{cases} x=0 \\وأ \\ x=-2 \end{cases} $$
أثبت أنه من أجل كل
لدينا
و منه :
- بين أن المنحنى يقبل مماسينوموازيين للمستقيم.
إذن :
- أكتب معادلة لكل من المماسين و.
أنشئ المستقيم
أحسب مساحة الحيز المستوي المحدد بالمنحنى
إذن :








