ادرس تغييرات الدالة
- حساب النهايات:
- دراسة إتجاه تغير الدالة
الدالة
أي أن
بماأن
وعليه لما
لما
- جدول التغيرات :
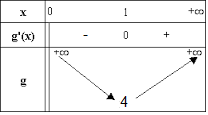
- استنتج إشارة على المجال
بما أن
فإنه من أجل كل
بين أنه من أجل كل
الدالة
وعليه
بماأن من أجل كل
إذن
احسب
لدينا :
ومنه
احسب
- جدول التغيرات:
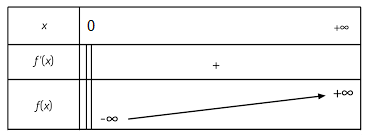
ليكن المستقيم
- احسب ،ثم فسر النتيجة بيانيا.
إن $$ \lim_{\substack{x \to +\infty}} [f(x)-\frac{1}{2}x] = \lim_{\substack{x \to +\infty}} [\frac{Ln x}{x} - \frac{1}{2x}] =0 $$
اذن المستقيم $$ (D) $$ مستقيم مقارب للمنحنى $$ (C_f) $$ بجوار $$ +\infty $$
- أدرس وضعية المنحني بالنسبة للمستقيم
من أجل كل
إذن
معناه
معناه
وعليه
ينتج أن
وبالتالي : في المجال
في المجال
لما
أنشئ المستقيم
أحسب بـ
$$ S=\int_1^{\sqrt{e}}[y-f(x)]dx+\int_\sqrt{e}^2[f(x)-y]dx $$
$$ S=\int_1^{\sqrt{e}}[-\frac{1}{x}Lnx+\frac{1}{2}\times\frac{1}{x}]dx+\int_\sqrt{e}^2[\frac{1}{x}Lnx-\frac{1}{2}\times \frac{1}{x}]dx $$
$$ S=-\int_1^{\sqrt{e}}\frac{1}{x}\times Lnx dx+\frac{1}{2} \int_1^{\sqrt{e}} \frac{1}{x}dx + \int_\sqrt{e}^2 \frac{1}{x}Lnx dx - \frac{1}{2} \int_{\sqrt{e}}^2 \frac{1}{x} dx $$
$$ S=-\Big[\frac{1}{2}(Lnx)^2\Big]_1^{\sqrt{e}} + \Big[\frac{1}{2}Lnx\Big]_1^{\sqrt{e}} + \Big[\frac{1}{2}(Lnx)^2\Big]_\sqrt{e}^2-\frac{1}{2}\Big[(Lnx)\Big]_\sqrt{e}^2 $$
$$ S=-\frac{1}{16}+\frac{1}{4}+\frac{1}{2}(Ln2)^2-\frac{1}{8}-\frac{1}{2}Ln2+\frac{1}{4} $$
$$ S=\frac{5}{16}+\frac{1}{2}Ln2\times(Ln-1) $$
نعتبر الدالة
- بين أن الدالة دالة زوجية.
من أجل كل $$ x \in \mathbb{R}* $$ ؛ $$ -x \in \mathbb{R}* $$ لأن $$ \mathbb{R}* $$ متناظرة بالنسبة إلى صفر
و $$ h(-x)=h(x) $$ لأن $$ |-x|=|x| $$ و $$ (-x)^2=x^2 $$
إذن $$ h $$ دالة زوجية
- اشرح كيفية رسم المنحني ثم أرسمفي المعلم السابق .
اذا كان
ونتم الرسم إلى
- استنتج حلول المتراجحة :
حلول هذه المتراجحة هي فواصل نقط تقاطع
وفواصل نقط
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
