- احسب و
- ادرس اتجاه تغير الدالة ، ثم شكل جدول تغيراتها .
إشارة
لدينا
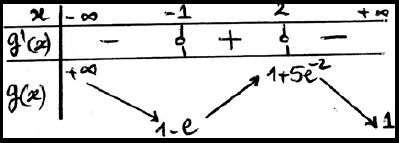
- بين أن للمعادلة حلين في، أحدهما معدوم و الآخرحيث
بيان أن المعادلة
لدينا
ولدينا الدالة
و
إذن حسب مبرهنة القيم المتوسطة ، المعادلة
حيث
- استنتج إشارة على
إشارة

- احسب و.
- بين أنه من أجل كل عدد حقيقي ،.( حيثهي الدالة المشتقة للدالة) .
بيان أنه من أجل كل
إذن
- شكل جدول تغيرات الدالة على، ( نأخذ) .
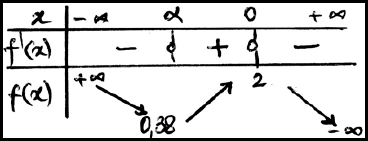
- عين دون حساب : ، ثم فسر النتيجة هندسيا .
تعيين
لأن
إذن نستنتج أن المنحنى
- بين أن المستقيم ذا المعادلةمستقيم مقارب مائل للمنحنىعند.
بيان أن المستقيم
إذن ، المستقيم
- ادرس وضعية المنحنى بالنسبة للمستقيم.
دراسة الوضع النسبي ل
لدينا
لدينا
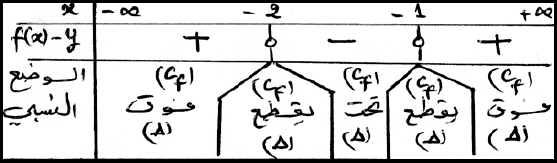
- بين أن للمنحنى نقطتي انعطاف يطلب تعيين إحداثيتهما .
بيان أن
لدينا
ومنه إشارة
بما أن
بما أن
- ارسم وعلى المجال.
- ناقش بيانيا و حسب قيم الوسيط الحقيقي عدد و إشارة حلول المعادلة :على المجال
و منه
إذن
عين الأعداد الحقيقية
تعيين الأعداد
لدينا
إذن
إذن
- احسب التكامل التالي : حيثعدد حقيقي موجب تماما و فسر النتيجة هندسيا .
حساب
ومنه
- احسب
حساب
إذن








