Le plan incliné de la figure 3 est composé de deux parties : la première,
Le diagramme des accélérations du mouvement qui en résulte est donné par la figure 4. On donne :
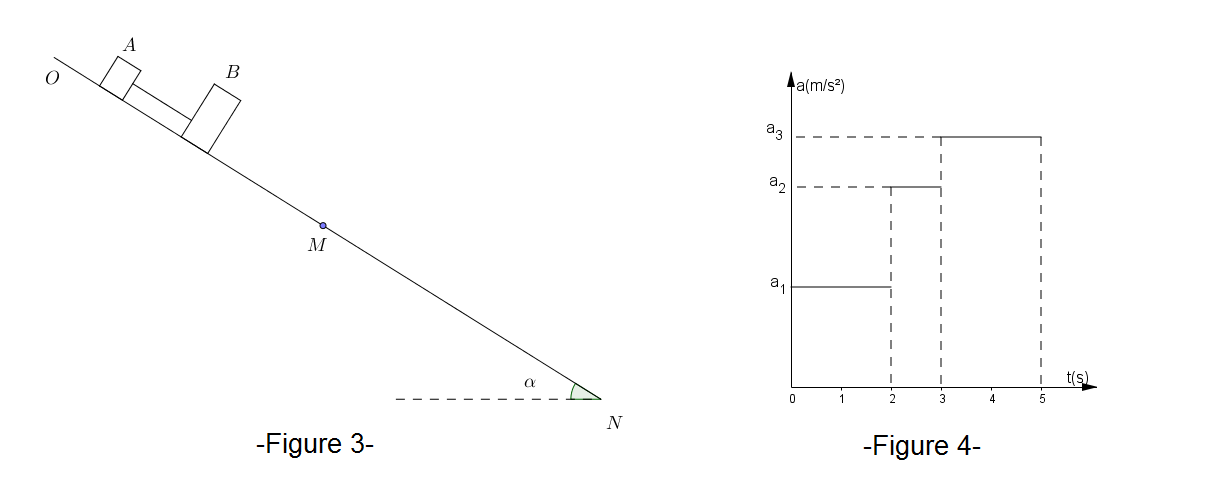
A quel instant,
Instants
On applique la relation fondamentale de la dynamique (RFD) au système
Par projection sur l’axe du mouvement :
On conclut que les changements d’accélération sont dus aux forces de frottements
Dans l’intervalle de temps
Calcul de l’angle
On applique la RDF sur
A partir de
On projette sur l’axe du mouvement :
Donc :
Dans l’intervalle de temps
- Représenter qualitativement les forces agissant sur chacun des deux corps durant cet intervalle de temps.
- Représentation des forces :
A est sur la partie rugueuse
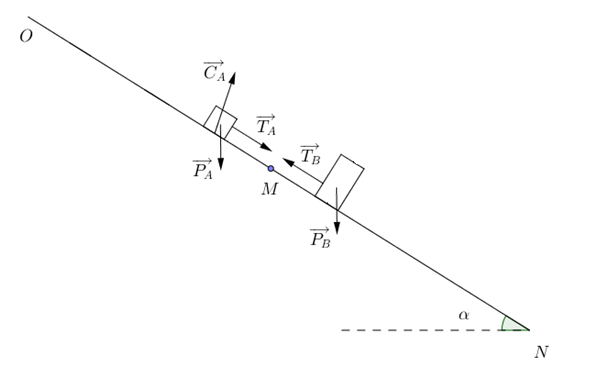
- Déterminer le coefficient de frottement dynamique , caractérisant le contacte entre le corps A et le tronçon (OM) de la piste.
- Détermination de :
On applique la RDF sur A :
Projection :
- Axe du mouvement : ..........(1)
- Axe normal :
On sait que
Donc
On applique la RDF sur B
Projection :
- l’axe du mouvement :
comme le fil est de masse négligeable :
On remplace
Dans l’intervalle de temps
Calcul de la tension du fil T pour
On applique la RDF sur A :
Projection :
- Axe du mouvement : .........(2)
- Axe normal :
De (2) :








