- Une piste ABC est constituée d'un tronçon AB incliné d'un angle par rapport à l'horizontale et d'un tronçon horizontale BC (voir figure 1).On place sur la partie AB un corps de masseLe contact entre le corps et le tronçon AB est caractérisé par le coefficients de frottements statiqueet dynamique.On donne
1.1- Pour quelle valeur de l'angle
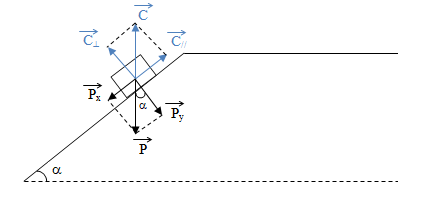
1.1- Détermination de l'angle de rupture d'équilibre:
On applique la relation fondaamentale de la dynamique au corps
On a, à partir de la figure :
Par projection
Sur l'axe du mouvement:
Sur l'axe normal:
1.2- Représenter dans ce cas les forces agissant sur la masse
1.2- Représentation des forces :
2. En réalité l'angle
2.1- Représenter qualitativement les forces agissant sur les masses
2.2- Calculer les modules des accélérations
2.2- calcul des modules des accélérations :
On applique la relation fondamentale de la dynamique (RFD):
On projette sur les axes de déplacement :
- Les fils sont inextensibles et de masses négligeables.
- La poulie est de masse négligeable .
Donc:
On sait que :
On remplace dans (1) :
On obtient:
2.3- Lorsque
- Etablir les expressions des travaux des forces agissant sur le corps au cours de son déplacement depuis le point "I" jusqu'à la compression maximale.
- Calculer la constante de raideur K du ressort.
- Travaux des forces agissant sur :
2. Calcul de la constante K:
D'après le théorème de l'energie cinétique :
avec:
et
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
