Parie 1
Un corps
On donne :
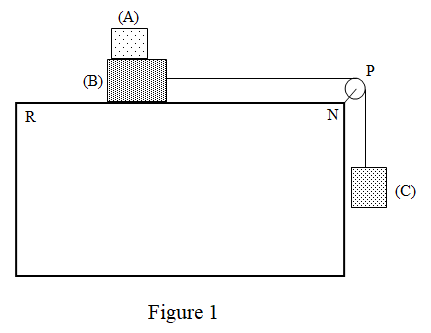
Représenter, qualitativement, les forces qui agissent sur chacun des trois corps à l’équilibre.
Représentation des forces :
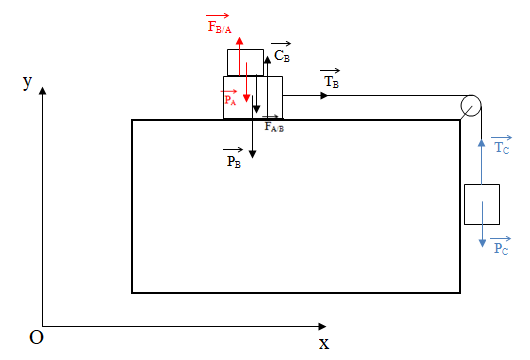
Trouver la valeur minimale
- Calcul de la valeur minimale :
On applique la relation fondamentale de la dynamique sur le corps
Par projection sur l’axe
On applique la RFD sur le système
Par projection sur Ox :
Sur
Les fils sont inextensibles
De (1), on a
De (3), on a
De (2), on a
Donc
Pour que le système se mette en mouvement, le corps C doit avoir une masse minimale de
Partie 2
Le corps
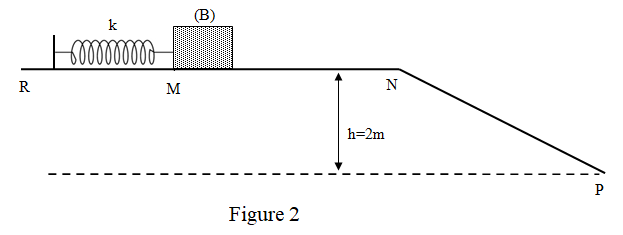
- On comprime le ressort de et on lâche le corps sans vitesse initiale. Trouver la vitesse du corps lorsqu’il atteint le point, extrémité du plan horizontal. On prendra la référence des énergies potentielles de gravitation au niveau du sol.
On donne :
Vitesse du corps au point N :
La partie
Le corps, abandonné sans vitesse initiale au point
Représentation des graphes
- Au point :
Le corps est abandonné sans vitesse initiale :
- Au point :
Il n’y a pas de frottements sur la piste








