On considère le mouvement d’une petite pièce A qui s’est détachée d’un missile B quatre secondes après le lancement de ce dernier. Les mouvements des deux corps ont lieu dans le plan (O,x,y) d’un système de coordonnées cartésiennes d’axe (Oy) vertical ascendant. Les origines des temps et des espaces correspondent à l’instant et à l’endroit du lancement du missile. La figure I représente les diagrammes des composantes
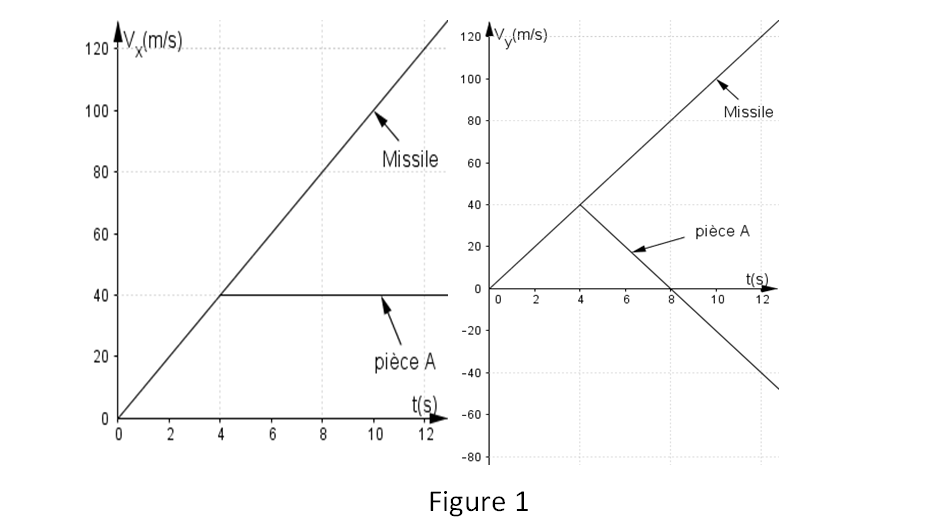
1- Déterminez :
- a- Les coordonnées du point d’altitude maximale atteint par A.
- b- Le vecteur vitesse moyenne de A dans l’intervalle de temps .
1.a- Coordonnées du point d’altitude maximale atteint par
Au point
On a alors :
Donc
b- Le vecteur vitesse moyenne :
Donc :
2- On se propose de déterminer les propriétés cinématiques du mouvement de
- Déterminez puis tracez les vecteurs position, vitesse et accélération, avec les échelles indiquées ci-dessous:
b. En déduire, sans calcul mais en justifiant votre réponse, les composantes intrinsèques de l’accélération.
2-a. Détermination des vecteurs :
- La position :
- La vitesse :
à
donc
- L’accélération :
- C’est la pente de la tangente au graphe
- C’est la pente de la tangente au graphe
2-b. Déduction des composantes intrinséques de l'accélération :
On a
Donc :
3- On décrit maintenant les propriétés du mouvement de
3-
4- Donnez les expressions des vecteurs vitesse et accélération de
4- Vitesse et accélération relatives :
- Soit le missile :
à t = 12 s :
La vitesse
L'accélération est :
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
