Exercice 2
Un bloc de masse
glisse, sans frottements, sur un rail formé d’une partie curviligne
et d’une boucle circulaire de rayon
(figure
).
On donne :
et
Question 1
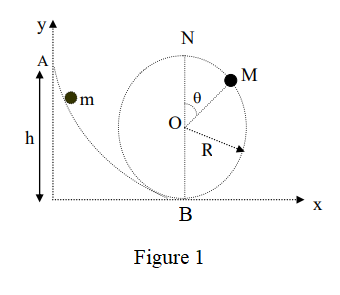
Le bloc est lâché sans vitesse initiale d’un point
situé à une hauteur
. Quelle est la vitesse
du bloc au point
?
Réponse 1
Détermination de la vitesse au point
:
Le bloc ne subit aucun frottement, la seule force qui s’exerce sur lui est son poids
qui est une force conservative. L’energie mécanique totale du bloc est donc constante.
Question 2
Le bloc aborde ensuite la partie circulaire
sur laquelle on repère sa position par l’angle
entre les points
et
. Quelle est l’expression de la vitesse du bloc au point
en fonction de
et
.
Calculer cette vitesse.
Réponse 2
Détermination de la vitesse au point
:
Il n’ y a pas de frottement sur cette partie non plus, d’après le théorème de l’énergie mécanique
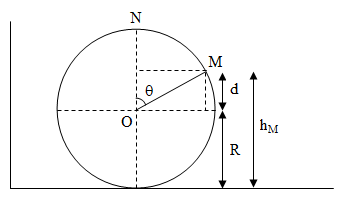
Donc
Question 3
a- En utilisant la relation fondamentale de la dynamique, déterminer l’expression de la force de contact
au point
en fonction de
et
.
b- Si
, en déduire alors l’angle
pour lequel le bloc quitte le rail.
Réponse 3
a- L’expression de la force de contact au point
:
On applique la relation fondamentale de la dynamique sur le bloc :
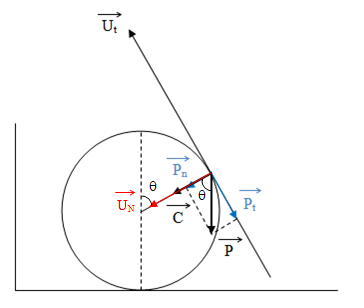
Projection sur
:
Projection sur
:
b- Le bloc quitte la piste si
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
