Deux corps
Les parties I, II et III sont indépendantes.
Le graphe donnant l’évolution de la vitesse en fonction du temps de la masse
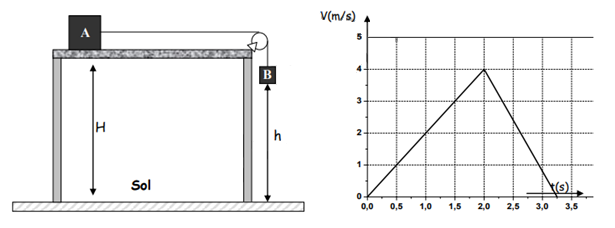
Tracer le diagramme de l’accélération en fonction du temps.
Diagramme
- :
- :
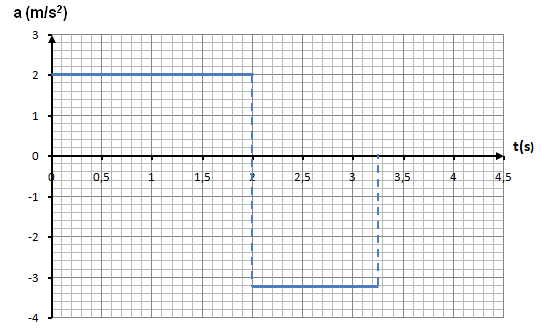
Déterminer la nature de chaque phase. Justifiez.
Nature du mouvement :
- :etmouvement rectiligne uniformément accéléré.
- :etmouvement rectiligne uniformément décéléré.
Déterminer la distance parcourue par
Distance parcourue par la masse
- phase :
On remarque que cette distance est égale à la hauteur initiale du corps
- phase :
Représenter le vecteur vitesse,
Vitesse de
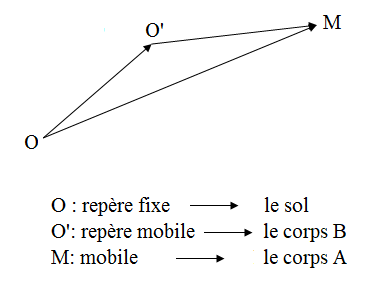
- A ,
- A le corpsest immobile au sol :
Donc
Du graphe
Calculer la valeur minimale de la masse
Masse minimale de
On applique la relation fondamentale de la dynamique sur le corps
Par projection sur
Sur
On applique la RFD sur le corps
Projection sur l’axe du mouvement :
De
De
De
En combinant ces relations avec
Pour que le système se mette en mouvement, le corps
On prend, maintenant, la valeur de la masse
a- Représenter qualitativement les forces agissant sur
b- En déduire l’expression des accélérations dans chaque phase. Donner leur valeur.
c- Exprimer et calculer la vitesse à la fin de la première phase.
a- Représentation des forces :
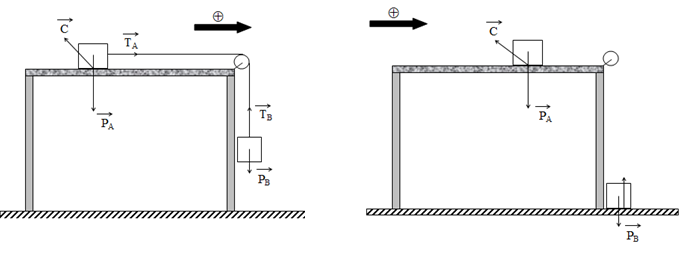
b- Les accélérations :
- phase :
On applique la RFD sur le corps
Par projection :
Sur
Sur
On applique la RFD sur le corps
Par projection sur l’axe du mouvement :
De
On a
On a alors :
- phase :
On applique la RFD au le corps
Projections :
Sur
Sur
c- Vitesse à la fin de la 1ère phase :
On a :
En multipliant les deux membres par
Comme
Alors
En intégrant
On trouve
Si la vitesse à la fin de la première phase est de
Le théorème de l’énergie mécanique totale en présence de frottements (forces non conservatives) donne
On prend le sol comme origine pour l’énergie potentielle
On a dit précédemment que la hauteur initiale de
Ce résultat correspond à la valeur donnée.
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
