Soit une couche sphérique uniforme de rayon
En utilisant le théorème de Gauss, déterminer le champ
- Champ à l'intérieur de la sphère:
On choisira donc comme surface de Gauss une sphère de rayon
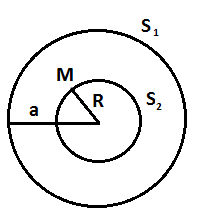
On sait qu'à l'intérieur d'une sphère le champ est radial
Théorème de Gauss:
On peut alors écrire:
La charge étant uniforme, le champ est constant en tout point de la sphère
ATTENTION: la surface ici est celle de la surface de Gauss, la sphère de rayon
On a alors
Les charges sont en surface de la sphère seulement,
- Champ à l'extérieur de la sphère:
la surface de Gauss est donc une sphère de rayon
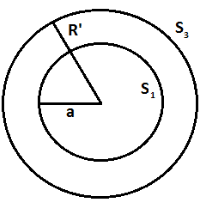
Théorème de Gauss:
Les charges qui sont en surface de la sphère
On a aussi
Donc
En déduire le potentiel
- Potentiel à l'extérieur de la sphère:
On connait la relation entre
On a vu que le champ était radial, donc
Les autres composantes sont nulles car comme on l'a vu précedemment, le champ ne dépend ni de
On sait qu’à l’infini le potentiel est nul
Donc l'expression du potentiel à l'extérieur de la sphère est :
- Potentiel à l'interieur de la sphère:
On détermine la constante en exprimant la continuité de
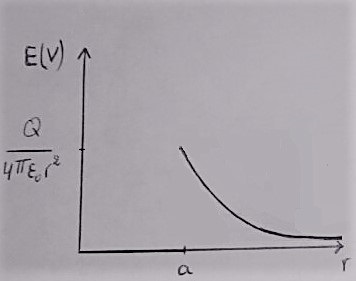
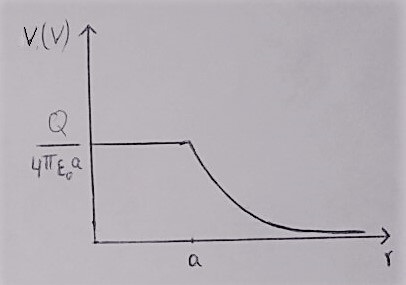
Tracer
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
