Exercice 3
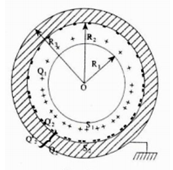
Une sphère conductrice (
) de rayon
est portée au potentiel
.
Question 1
Calculer sa charge
.
Réponse 1
d'ou
Le potentiel
étant positif,
Question 2
On isole (
) de la source de potentiel, puis on l’entoure d’une autre sphère (
), initialement neutre, isolée et concentrique à (
) de rayon intérieur
et extérieur
.
Trouver les charges totales des deux sphères et les charges portées par les faces de (
).
Réponse 2
: charge totale de (
)
: charge totale de (
)
: charge de la face interne de (
)
: charge de la face externe de (
)
(
) entoure (
), l’influence est donc totale
On a vu dans la première question que
était positive, donc
(
) était initialement neutre et isolée donc
(la charge se conserve)
, on a donc
Question 3
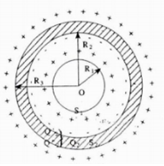
On relie maintenant (
) au sol. Que deviennent les charges totales de (
) et de (
) ainsi que les charges portées par les faces de (
) ?
Réponse 3
La sphère (
) est reliée à la terre, donc
La sphère (
) porte toujours la même charge (
)
L’influence est totale,
donc
d’où
La sphère (
) se charge donc négativement
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
