Exercice 6
Deux cylindres métalliques
et
de même axe
, de même hauteur
et de rayon
et
tel que
portent des charges réparties uniformément en surface
(à l’extérieur de
) et
(à l’intérieur de
).
Question 1
Déterminer
par les méthodes classiques de l’électrostatique
Réponse 1
Soit
le potentiel de
et
le potentiel de
, en raisons des symétries des cylindres, le champ électrique est radial dirigé comme sur la figure de
vers
(soit
)
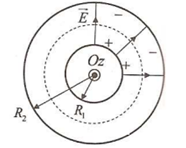
Le champ étant radial, on peut écrire :
On applique le théorème de Gauss à la surface formée par le cylindre de rayon
et de hauteur
et
sont collinéaires donc
(
est la surface d'un cylindre)
D'ou
(
est le vecteur unitaire radial)
Question 2
Déterminer le potentiel
entre les deux cylindres
Réponse 2
On sait que
et comme le champ est radial,
donc
En intégrant entre les limites
et
(
)
Question 3
En déduire la capacité de ce condensateur cylindrique
Réponse 3
La capacité
est le rapport de la charge de l’armature positive
à la différence de potentiel positive entre les deux armatures
:
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
