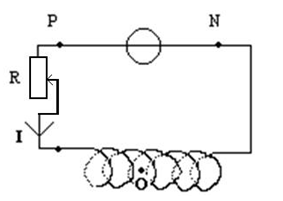
On dispose du montage suivant ci-dessous:
A l’aide d’une sonde à effet Hall et d’un teslamètre, on mesure le champ magnétique à l’intérieur du solénoïde en fonction de l’intensité. Le solénoïde a un nombre total de 1
On obtient les résultats suivants :
| B(mT) | 0,2 | 0,34 | 0,48 | 0,67 | 0,79 | 1,8 | 1,64 | 1,92 | 2,22 |
| I(A) | 0,15 | 0,25 | 0,36 | 0,49 | 0,58 | 0,92 | 1,18 | 1,37 | 1,59 |
Donnée :
Représenter graphiquement,
On obtient la droite suivante :
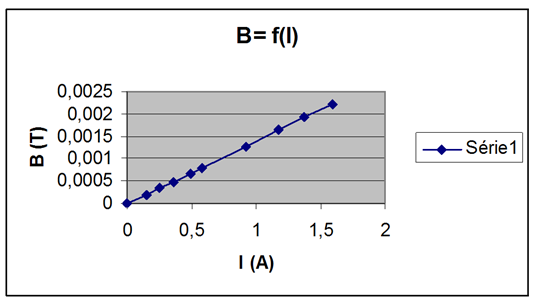
On a obtenu une droite passant par l’origine. Il y a donc une relation de proportionnalité entre
Le coefficient directeur de cette droite est
L’équation obtenue pour la droite est donc
Donner la relation reliant
A l’aide de l’équation de la courbe, déterminer la longueur de ce solénoïde et en déduire le nombre de spires par mètre
On a
La longueur du sélénoide est donc donnée par la relation:
Le nombre de spire par mètre est :
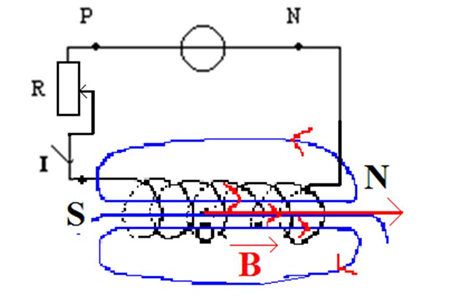
Représenter quelques lignes de champ orientées, à l’intérieur et à l’extérieur du solénoïde ainsi que le vecteur
On obtient le vecteur