Une sphère
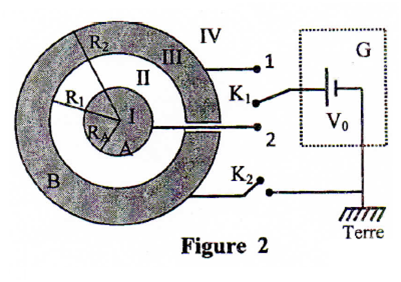
Le générateur est relié au conducteur
a- Représenter, qualitativement, la répartition des charges qui apparaissent sur les conducteurs
b- Calculer les charges
a- Représentation des charges:
Le générateur est relié au conducteur
Des charges
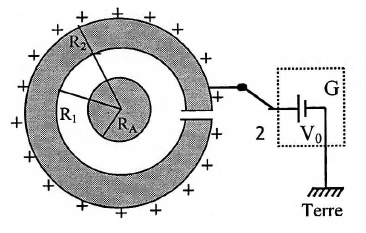
b- Calcul des charges:
Le commutateur
Représenter, qualitativement, la nouvelle répartition des charges qui apparaissent sur les deux conducteurs
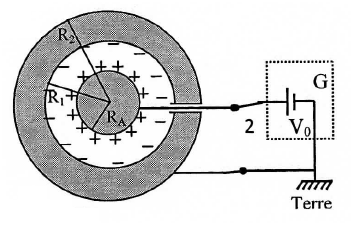
Une charge
La liaison de
Déterminer les expressions du champ et du potentiel électriques dans les régions
Les expressions du champ électrique dans les différentes régions de l’espace :
On choisit comme surface de Gauss une sphère de rayon
Pour des raisons de symétrie, le champ est radial :
Donc
- :
- :
- :
- :
Les potentiels dans les différentes régions :
On a
- (à l’infini le potentiel est nul)
Calculer les nouvelles charges
Calcul des nouvelles charges :
Pour
Les deux conducteurs, ainsi montés, forment un condensateur sphérique. Déterminer l'expression de sa capacité électrique. Que devient cette expression si les valeurs de
Détermination de la capacité du condensateur formé :
Dans le cas où








