On considère le circuit électrique, représenté par le schéma de la figure
Données :
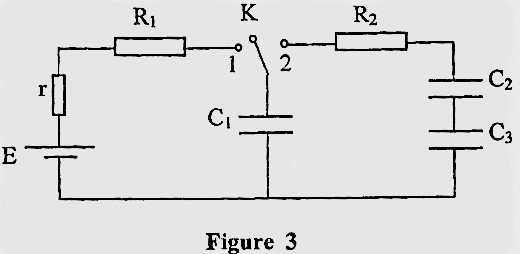
A l’instant
a- Etablir l’équation différentielle régissant la charge du condensateur
b- En déduire l’expression de la charge
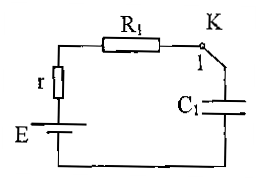
a- L’équation différentielle régissant la charge :
On a alors :
b- Déduction de l'expression de la charge
Pour avoir l’expression de la charge
L’équation homogène :
Quand
A
On a alors
On remplace dans l’équation différentielle :
L’équation de la charge s’écrit donc :
Déterminer l’expression du courant
L’expression du courant :
Donc
Faire le bilan énergétique du circuit.
Le bilan énergétique du circuit :
- Energie fournie par le générateur :
- Energie stockée par le condensateur : :
- Energie consommée par effet joule :
Le condensateur
Lorsque l’équilibre électrique est établi, calculer :
a- La d.d.p aux bornes du condensateur
b- Les charges de chacun des condensateurs
c- La d.d.p aux bornes de chacun des condensateurs
d- L’énergie perdue par effet joule dans le circuit.
- Le condensateur est totalement chargé etest en position:
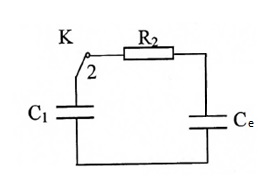
a- La d.d.p aux bornes de
b- Les charges des condensateurs :
c- Les d.d.p aux bornes de
d- L’énergie dissipée dans
- Energie stockée dans le condensateur :
- Energie stockée dans le condensateur :
- Energie consommée par effet Joule dans :
En appliquant la conservation de l'énergie à un instant
l'énergie dissipée par effet joule dans la résistance








