On considère le circuit électrique, représenté sur la figure ci-dessous, formé de deux générateurs de
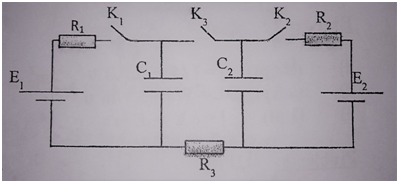
Partie
L’interrupteur
Montrer que le courant traversant la résistance
Soit
Etablir les équations différentielles régissant l’évolution de la charge des condensateurs
Les équations différentielles régissant les charges
Maille
L’équation différentielle régissant la charge du condensateur
Maille
De la même façon, on trouve l’équation différentielle régissant la charge du condensateur
En déduire l’expression des charges
Les expressions des charges
On résout les équations différentielles précédentes :
On pose
On résout d’abord l’équation homogène :
Quand
Donc
On remplace dans l’équation différentielle :
D’où
On a alors,
De la même manière on trouve l’expression de
Calculer à l’équilibre la charge totale emmagasinée dans les deux condensateurs.
L’énergie emmagasinée :
- L’énergie emmagasinée dans :
- L’énergie emmagasinée dans :
- L’énergie totale emmagasinée :
Partie
On ouvre les interrupteurs
Calculer à l’équilibre la charge finale portée par chaque condensateur.
Calcul des nouvelles charges :
Il y a conservation des charges :
Donc
La d.d.p aux bornes de chaque condensateur est la même
D’où
Calculer l’énergie totale finale emmagasinée dans le système des deux condensateurs. En déduire l’énergie dissipée par effet Joule.
L’énergie finale emmagasinée dans les deux condensateurs :
L’énergie dissipée par effet Joule :
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
