Etablir l’expression du champ magnétique créé par un fil infini parcouru par un courant
Champ magnétique créé par un fil infini traversé par un courant
On applique le théorème d’Ampère :
les coordonnées adaptées à ce problème sont les coordonnées cylindriques.
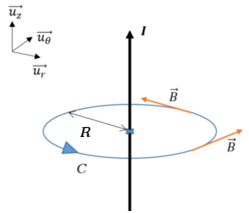
On choisira donc comme éléments de longueur pour le calcul, le cercle
On peut alors écrire :
D’où
(
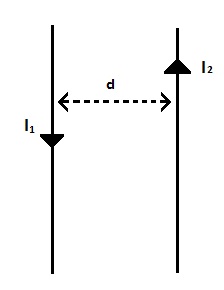
Deux fils parallèles et infinis distants de
Calculer la force par unité de longueur qu’exerce chacun des fils sur l’autre. Représenter ces forces à l’échelle
(
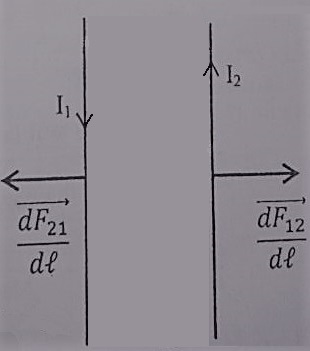
Force de Laplace par unité de longueur :
Représentation :
Les courants sont de sens opposés, les forces sont donc répulsives. Les vecteurs mesurent
Donner l’expression de l’intensité du champ magnétique résultant
On place dans le plan des deux fils un cadre rigide rectangulaire, susceptible de tourner autour d’un axe
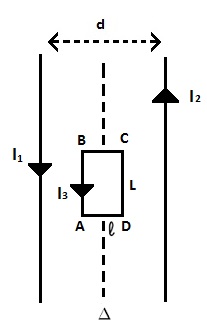
Représenter qualitativement les forces magnétiques appliquées sur chaque côté du cadre.
Représentation des forces agissant sur le cadre :
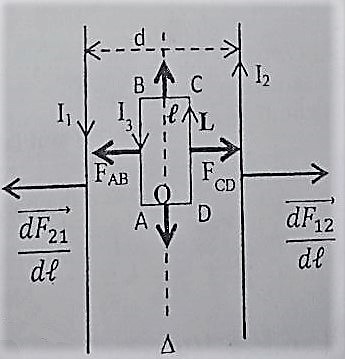
Calculer l’intensité des forces de Laplace exercées sur les côtés
Les intensités
Calculer le moment du couple agissant sur le cadre. Que peut-on conclure ?
Le moment du couple agissant sur le cadre :
Conclusion :








