Un pendul simple est constitué d’une boule de masse
Donner l’expression du moment cinétique
L’expression du moment cinétique :
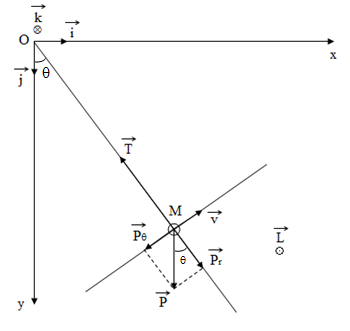
a- En appliquant le théorème du moment cinétique à la boule, montrer que, dans le cas des faibles oscillations, le mouvement du pendule est régi par l’équation différentielle :
b- Sachant que
a- Démonstration de l’équation différentielle :
Théorème du moment cinétique :
Bilan des forces :
Donc
On a vu que
On a alors
Dans le cas de faibles oscillations, on peut faire l’approximation suivante :
On obtient alors l’équation différentielle caractéristique du pendule :
La solution de cette équation différentielle est du type :
Avec
Expression de
En injectant les expressions de
On a alors
Remarque :
L’équation différentielle devient :
b- Calcul de la période d’oscillation du pendule :
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
