Exercice 1
Une particule de masse
se déplace le long d’un axe
sous l’action d’une force
dérivant d’un potentiel telle que
. La variation de son énergie potentielle en fonction de sa position est donnée par le graphe ci-contre.
Question 1
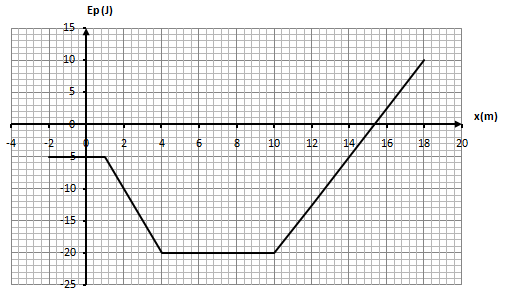
Tracer le graphe donnant la variation de
en fonction de
.
Réponse 1
On trace le graphe
dérive d’un potentiel, on peut écrire :
D’où
Question 2
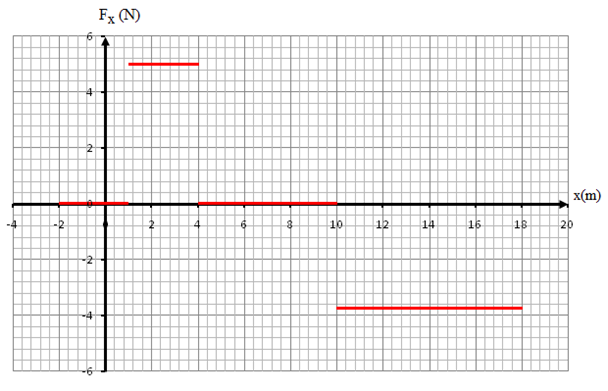
On abandonne la particule à
sans vitesse initiale. Tracer le graphe donnant la variation de son énergie cinétique en fonction de
.
Réponse 2
Graphe
A l’état initial :
et
Ce qui donne
La force à laquelle est soumise la particule dérive d’un potentiel, elle est conservative. D’après le théorème de l’énergie mécanique :
On a alors
Question 3
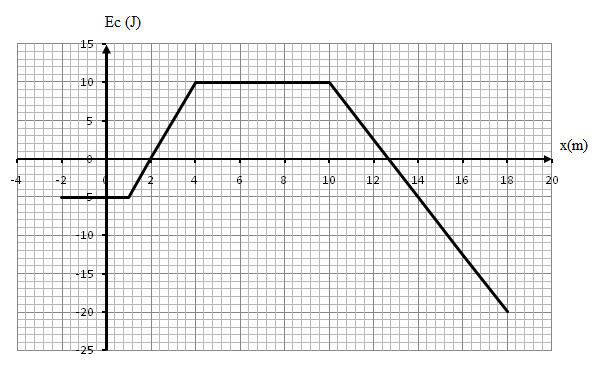
a- Dans quelle région le mouvement de la particule est-il possible ? Justifier votre réponse.
b- Décrire qualitativement le mouvement de la particule dans cette région.
Réponse 3
a- Le mouvement de la particule est possible pour
, c'est-à-dire
b- Mouvement de la particule :
partie
:
augmente donc
augmente
la particule accélère.
partie
:
et donc
, le mouvement est rectiligne uniforme.
partie
:
diminue donc
diminue
la particule ralentit.
On peut alors dire que le mouvement est oscillatoire.
قم بالدخول للإطلاع على المزيد من المحتوى
لتتمكن من الوصول إلى جميع الدروس والتمارين والمسابقات والفيديوهات وتصفح الموقع براحة قم بالدخول أو بتسجيل حساب مجانا.
