On abandonne sans vitesse initiale un bloc de masse
On note
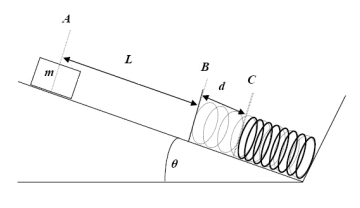
Démonter que l’énergie potentielle élastique
La force élastique dérive d’un potentiel
En choisissant comme origine de l’énergie potentielle
Par conséquent :
Rappeler le théorème de l’énergie mécanique totale. Que peut-on dire de l’énergie mécanique pour le système étudié ?
Théorème de l’énergie mécanique totale :
Les frottements sont dits négligeables, le théorème donne :
L’énergie mécanique totale d’une particule soumise à des forces conservatives est constante.
Donner les expressions des énergies totales aux points
Les énergies totales en
On choisi le point
Le bloc est abandonné sans vitesse initiale donc
Au point
Déduire l’expression de la constante de raideur
L’expression de la constante
L’énergie mécanique totale est constante au cours du mouvement
Si maintenant le contact entre le corps et le plan incliné est caractérisé par un coefficient de frottements
La hauteur maximale :
En présence de frottement, la variation d’énergie mécanique totale devient :
Soit
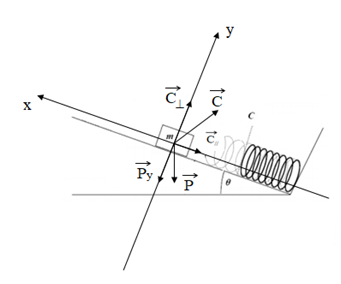
On applique la relation fondamentale de la dynamique sur le bloc :
Par projection sur l’axe
On sait que
On a alors
Ce qui donne
La hauteur :








