الإستمرارية
نقول عن
الدالة
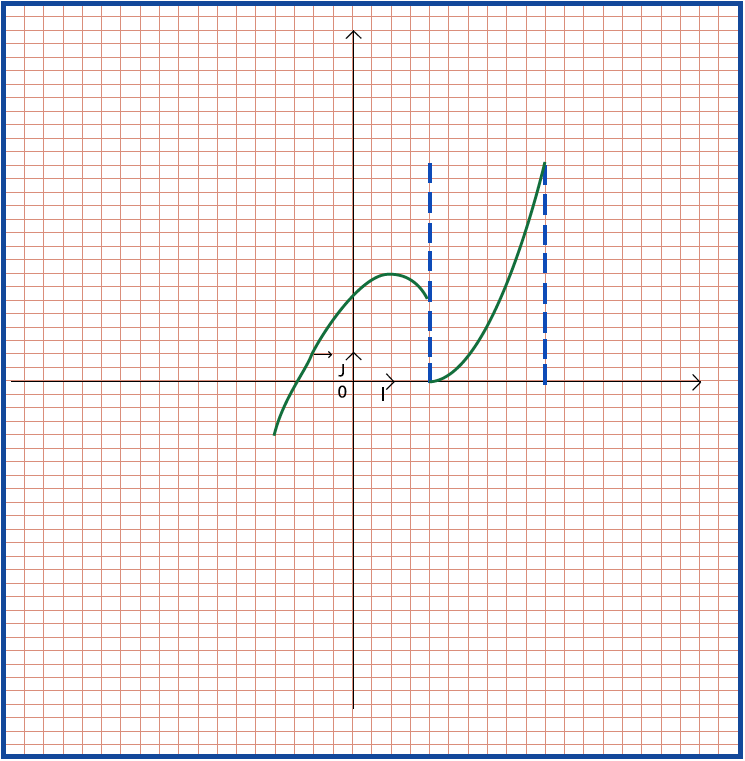
الدالة
الممثلة في الشكل المقابل مستمرة على المجال
لأن تمثيلها البياني مستمر و يمكن رسمه دون رفع اليد.
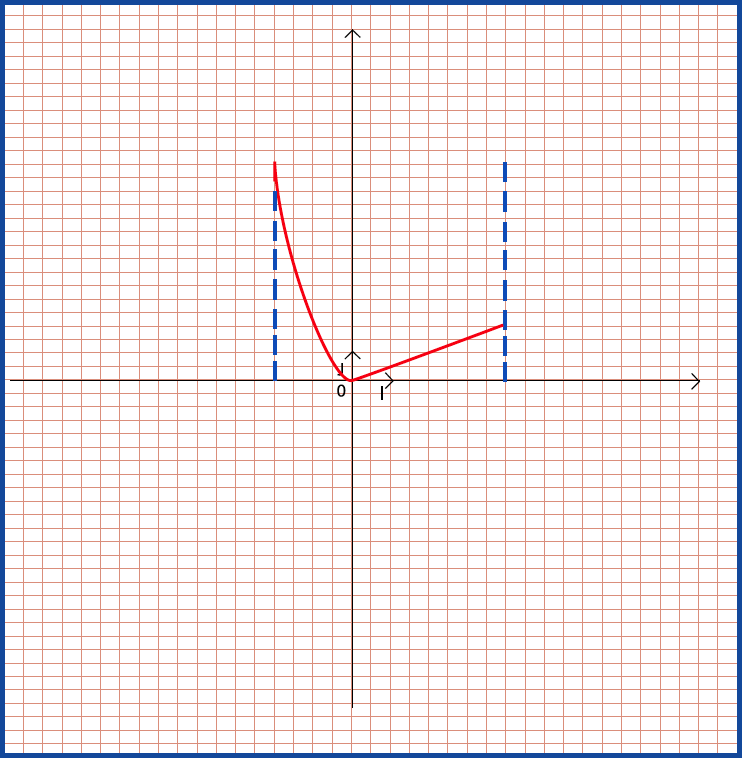
- الدوال المرجعية مستمرة على كل مجال من مجموعة تعريفها
- الدوال كثيرات الحدود مستمرة على
- الدوال الناطقة مستمرة على كل مجال من مجموعة تعريفها
- الدالة مستمرة على.
- الدالة مستمرة على كل من المجالينو
(نظرية مقبولة) لتكن
يوجد على الأقل عدد حقيقي
او يمكن القول : من أجل كل عدد حقيقي
المعادلة
بوضع
و لدينا :
إذن حسب نظرية القيم المتوسطة المعادلة
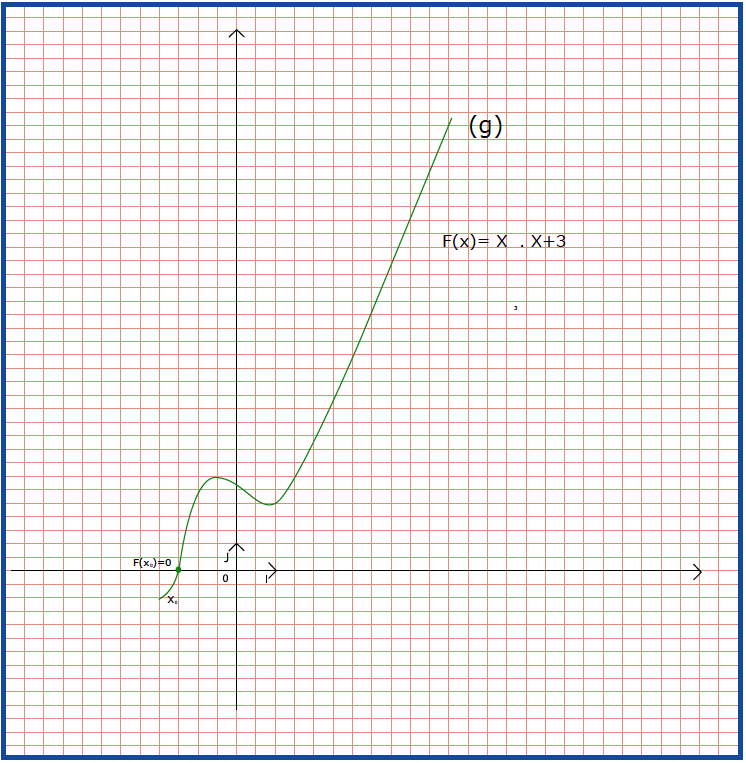
لتكن
إذن يوجد عدد وحيد
نقول أن المعادلة
تعمم نظرية القيم المتوسطة في حالة
نعتبر الدالة
- شكل جدول تغيرات الدالة
- أثبت أن المعادلة تقبل حلا وحيدًاحيث
- على
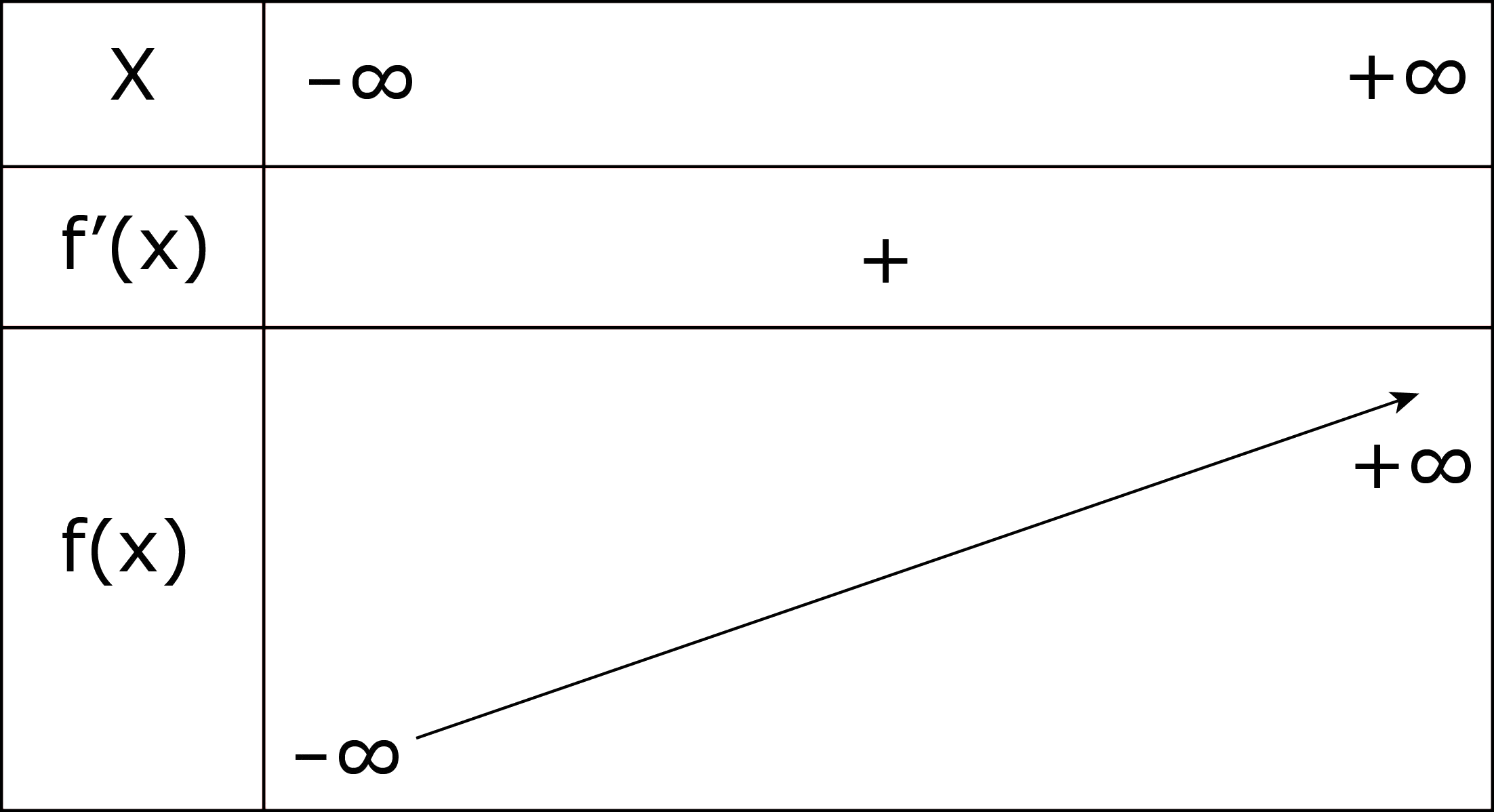
- الدالة مستمرة و متزايدة تماما على، فهي مستمرة و متزايدة تماما على المجالو لدينا :
شروط نظرية القيمم المتوسطة محققة إذن المعادلة
- إختبارات
- 10
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- lokmane LOKMANE
- 240 نقطة
-

- nacer-eddine benhaddad
- 200 نقطة
-

- soumia bessaad
- 200 نقطة
-

- Zergoug Safaa
- 195 نقطة
-
- مريم جلولي
- 185 نقطة
-

- صاره لعسلوجي
- 177 نقطة
-

- anis messai
- 172 نقطة
-

- Mahmoud mouslem Medkour
- 167 نقطة
-

- imadrass imadrass
- 163 نقطة
-

- Ikram AMRANE
- 160 نقطة
-









