المعادلة الديكارتية لمستوى في الفضاء
- معرفة الشعاع الناظم لمستوي
- كتابة المعادلة الديكارتية لمستوي
نسمي شعاع ناظم لمستوي
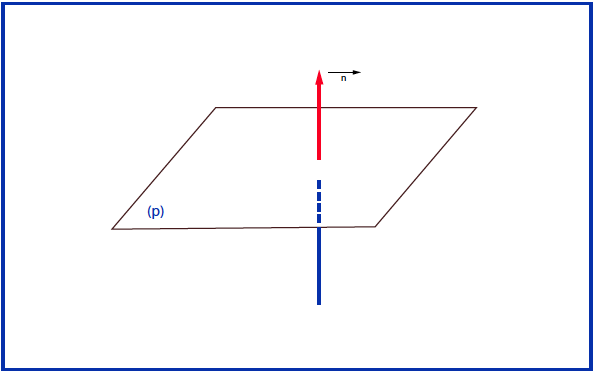
إذا كان
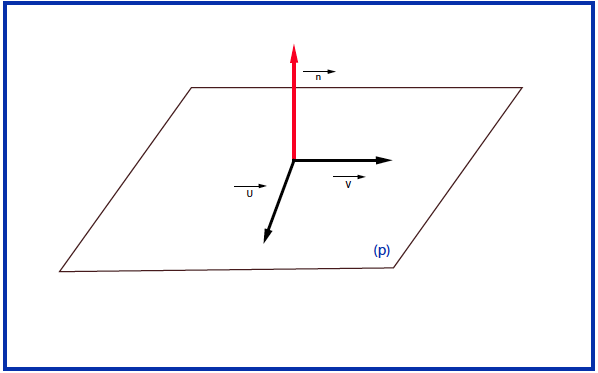
في معلم متعامد و متجانس كل مستو له معادلة من الشكل
و بالعكس :
في معلم متعامد ومتجانس لإيجاد معادلة ديكارتية لمستوي من الشكل
نتبع الطريقة التالية:
- نعرف الشعاع العمودي علىوفنتحصل على شعاع ناظمي للمستويو على المعاملاتللمعادلة المطلوبة
ليكن في معلم متعامد و متجانس النقط:
- تبيين أن معادلة المستوي هي :
لدينا
إذن النقط
التي تكافئ
بالجمع نجد:
بالطرح نجد:
منه :
إذا كان
معادلة المستوي
في معلم متعامد و متجانس. نعتبر المستوي
في المعلم المتعامد و المتجانس :المسافة بين النقطة
- إختبارات
- 8
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- lokmane LOKMANE
- 175 نقطة
-

- فاروق بن رقية
- 160 نقطة
-

- Misu Lzn
- 160 نقطة
-
- Bernard Farid
- 160 نقطة
-
- yasmine agrane
- 155 نقطة
-

- Bouallal Yacine
- 140 نقطة
-

- محمد نعمان جمعي
- 137 نقطة
-
- rym ch
- 135 نقطة
-

- layen layen
- 120 نقطة
-

- Fatima Ghawtia
- 114 نقطة
-









