الحساب لتكاملي:حساب المساحات
توظيف التكامل لحساب مساحة سطح معطى
- نعبر عن المساحات بوحدة المساحة
لتكن
لتكن
- مساحة الحيز من المستوى و الذي نرمز له بالرمز هو الحيز المحدد بالمستقيمالمنحنىو المستقيمات ذوي المعادلاتو
- نرمز بـ للجزء من الحيز الواقع فوق محور الفواصلأيموجبة
و بـ
أي أن:
و
إذن لدينا :3حالات.
إذن مساحة
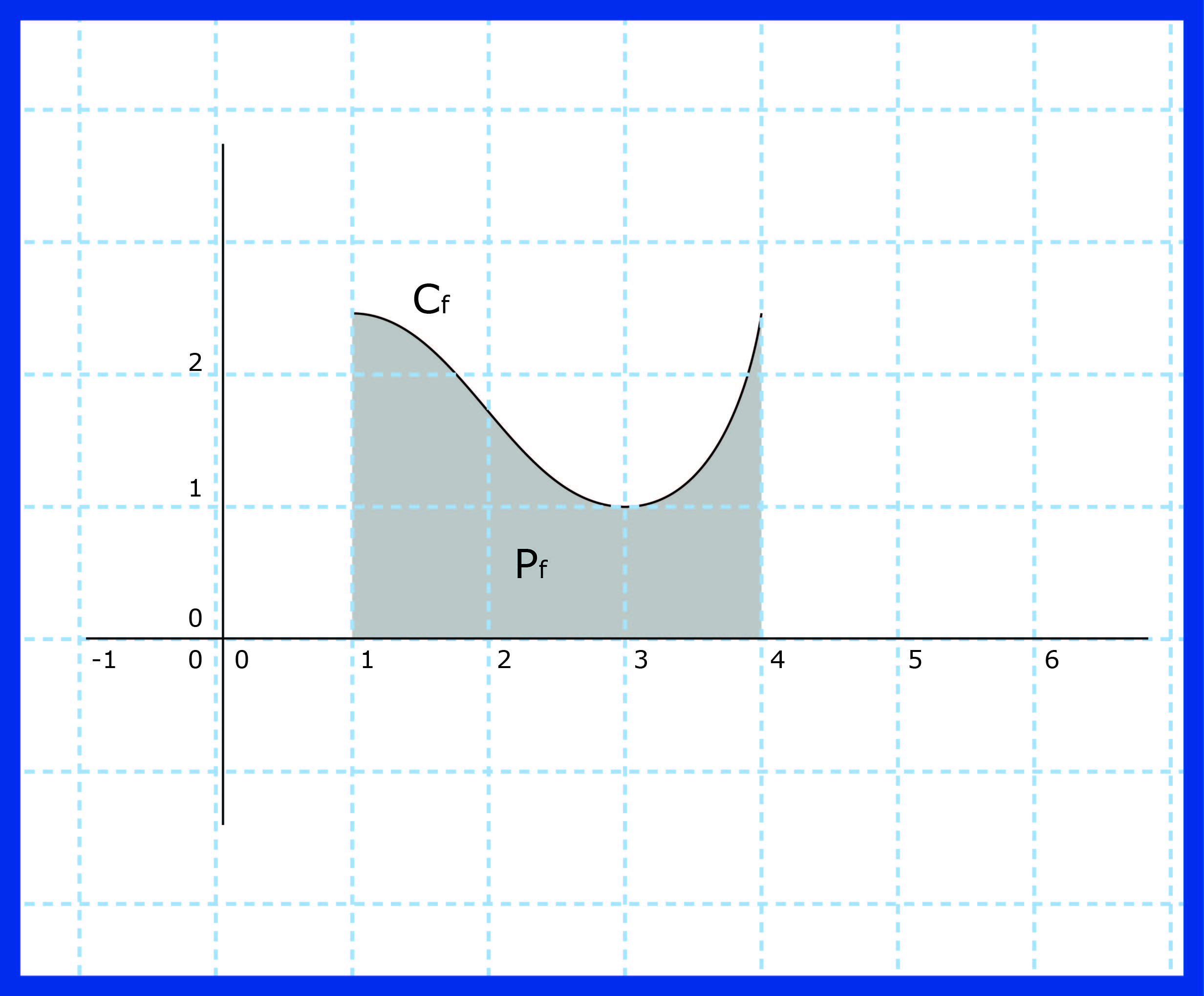
إذن مساحة
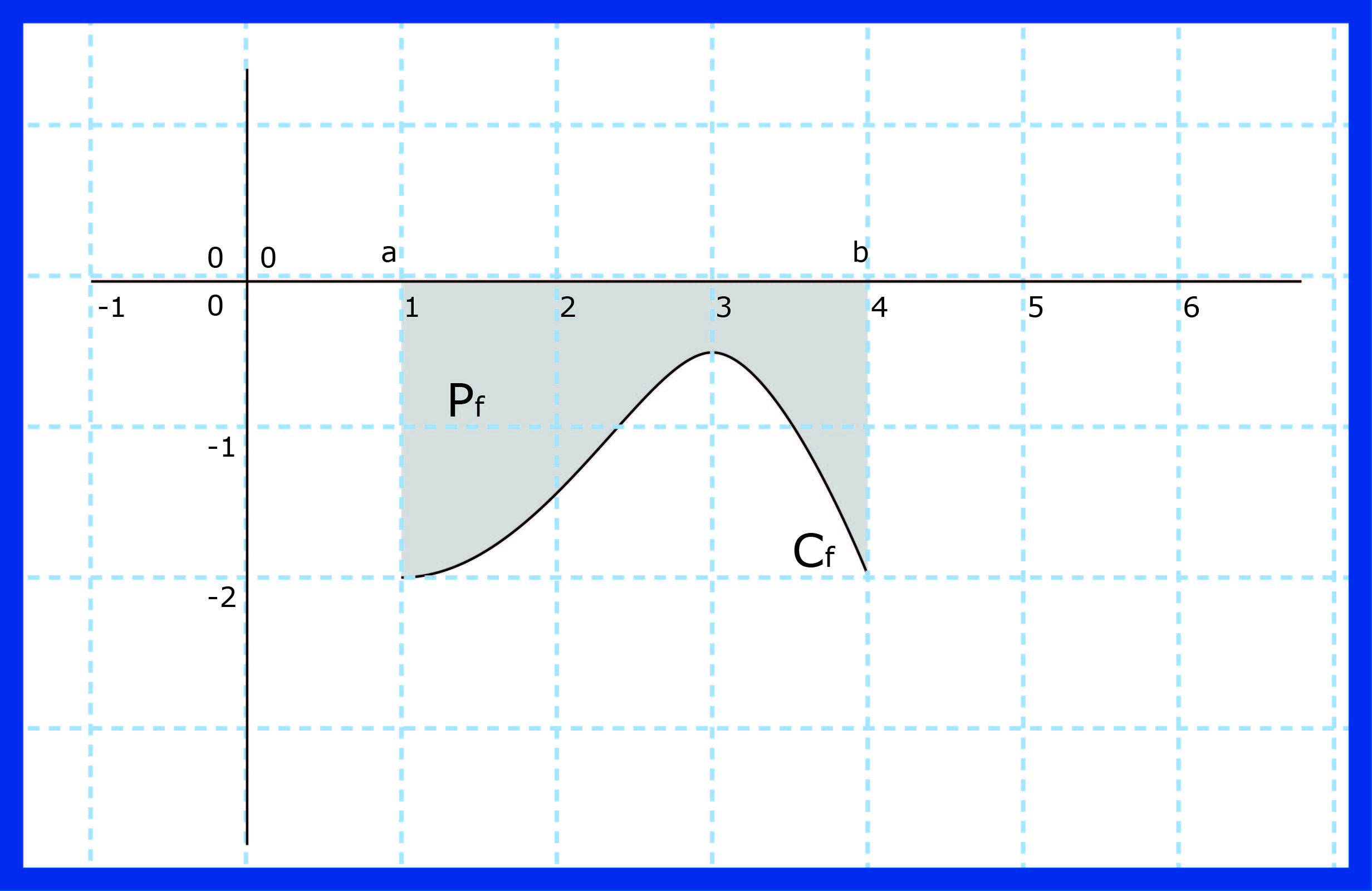
إذن مساحة
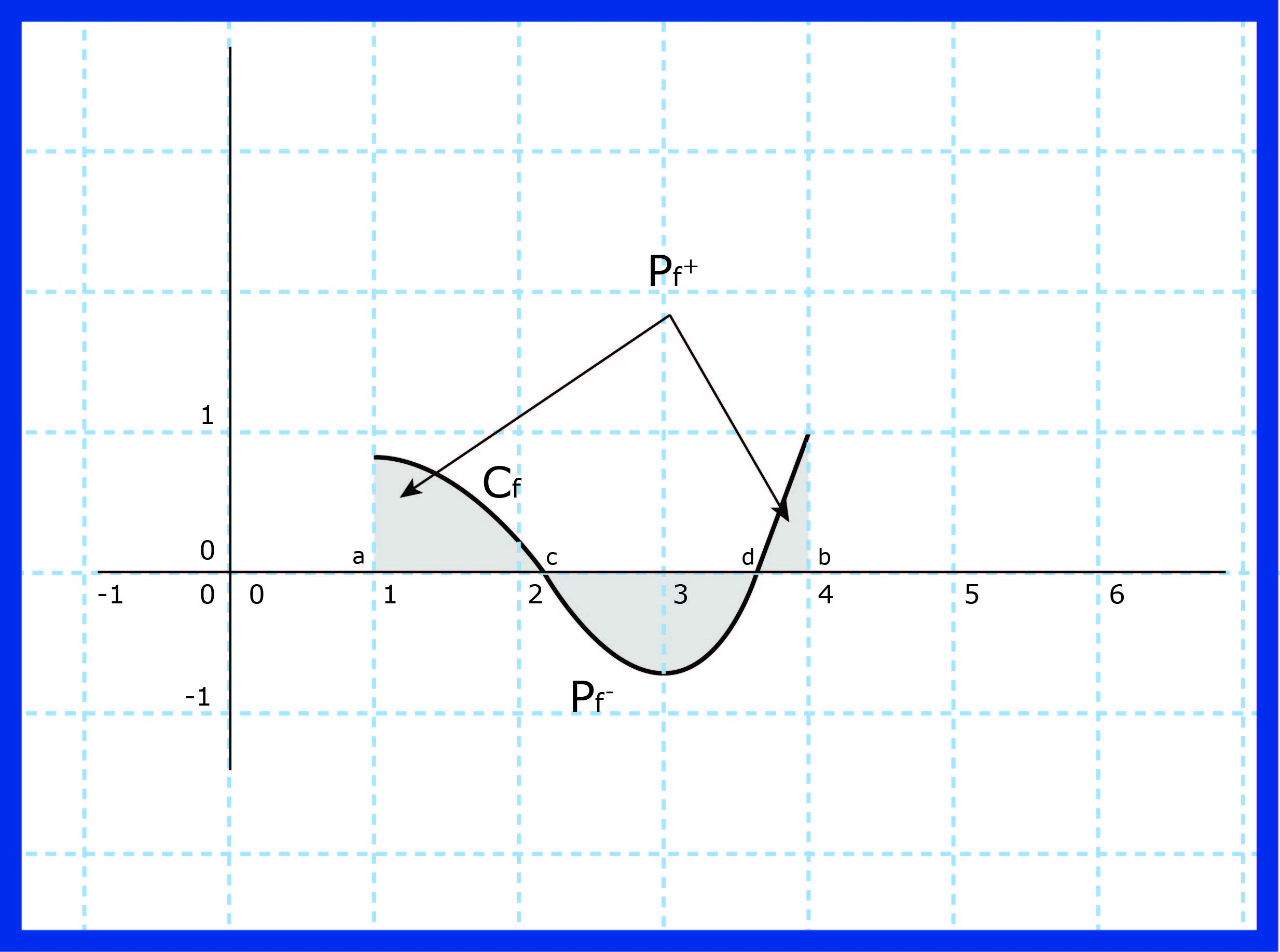
ليكن
ممثلتان بالمنحنيين
ليكن
-إذا كانت
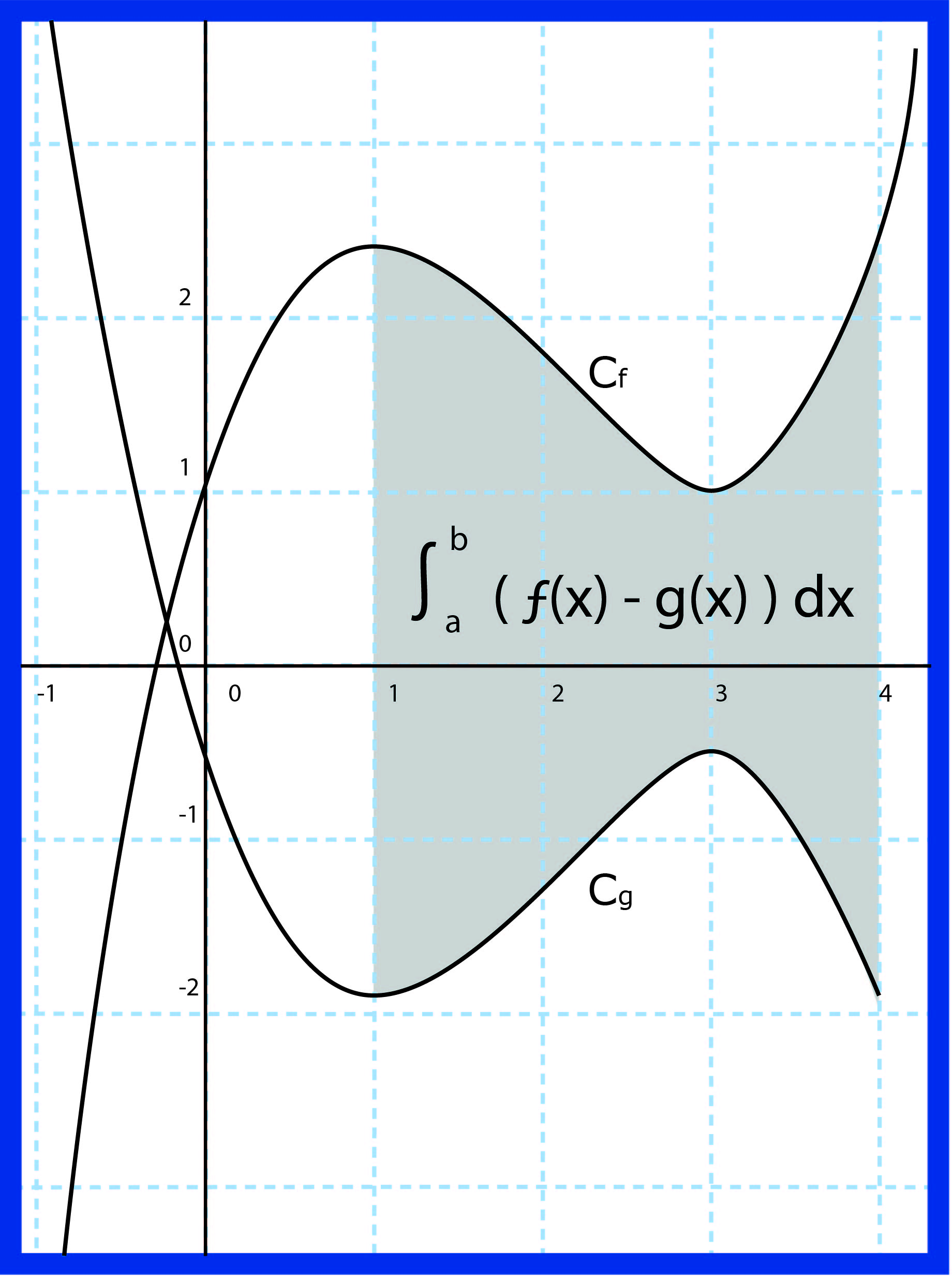
- إختبارات
- 3
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- Salah Adel
- 60 نقطة
-
- Bàlor Finn
- 60 نقطة
-
- ra sa
- 60 نقطة
-

- Hab Ré
- 38 نقطة
-
- Mekkaoui Tarek
- 37 نقطة
-
- abderahim op13
- 21 نقطة
-

- Khälęd Khëlīfã
- 20 نقطة
-
- Randy Oussama
- 15 نقطة
-
- bensiahmed abderrahmen
- 3 نقطة
-

- Boughazi Hassen
- 0 نقطة
-









