العد القوائم الترتيبات التبديلات
نسمي قائمة ذات عنصرا
إذا أردنا ان تكون هذه العناصر المرتبة متمايزة مثنى مثنى عندئذ لا يمكن للقائمة ان تحتوي أكثر من
- من أجل كل عدد طبيعي عدد قوائمذاتعنصرا يساوي
بينما يكون عدد قوائم
هذا الجداء يحوي
في الحالة الأولى (عدم اشتراط تمايز العناصر) يكون لكل عنصر من العناصر القائمة
في الحالة الثانية (قوائم عناصرها متمايزة مثنى مثنى ) يكون للعنصر الأول
نسمي القائمة التي عناصرها متمايزة مثنى مثنى ترتيبة و يرمز لعدد الترتيبات ذات
- ما عدد الأعداد ذات أرقام و التي يمكن تشكيلها من الأرقام:
- ما عدد الأعداد ذات أرقام متمايزة مثنى مثنى و التي يمكن تشكيلها من الأرقام:
- كل عدد هو قائمة ذات عناصر من بين الأرقامعدد الأعداد هو:
- كل عدد هو ترتيبة عناصر متمايزة من بين الأرقام
عدد الأعداد هو:
ترتيبة ذات
يمكن كتابة عدد الترتيبات ذات
مجموعة منتهية ذات
نسمي توفيقة ذات
نرمز لعدد التوفيقات ذات
- نلاحظ أن أي أن عدد الأجزاء التي تحوي عنصرا واحدا من مجموعة ذاتعنصرا هو
بينما
من أجل كل عددين طبيعيين
من أجل كل توفيقة ذات
- نريد تشكيل لجنة ذات تلاميذ من بينتلميذا ، ما عدد اللجان التي يمكن تشكيلها؟
كل لجنة هي توفيقة ذات
- من أجل كل عددين طبيعيين وحيثلدينا:
- من أجل كل عددين طبيعيين وحيثلدينا:
- عدد الأجزاء التي تحوي عنصرا هو عدد متمماتها التي تحويعنصرا.
- عدد الأجزاء ذات عنصر التي تحوي العنصرهوو عدد الأجزاء ذاتعنصر و التي لا تحويهوو بالتالي فعدد الأجزاء ذاتعنصر هوو هو
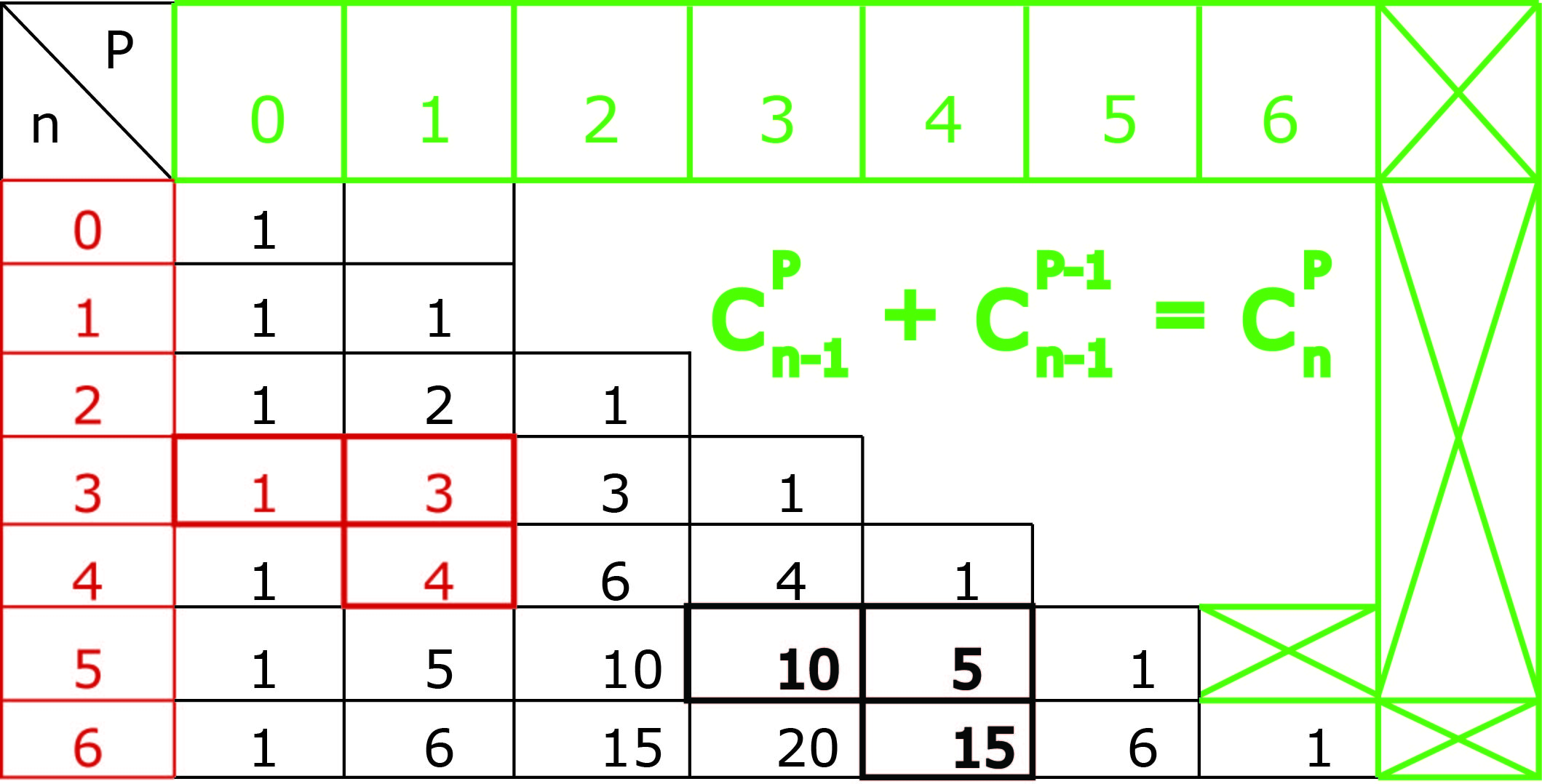
تمكننا الخاصية الثانية من حساب
أحسب المجموعتين :
باستعمال دستور ثنائي الحد نلاحظ أن:
- و









