دراسة ظواهر كهربائية
هو كل تيار كهربائي شدته ثابتة بدلالة الزمن.
هو كل تيار كهربائي شدته متغيرة بدلالة الزمن.
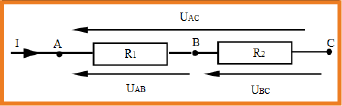
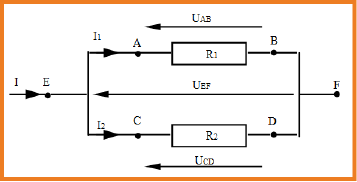
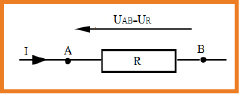
ملاحظة : يجب التفريق بين مولد التوتر ومولد التيار .
مولد التوتر : تبقى
مولد للتيار : تبقى
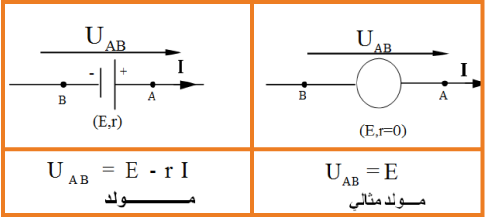
تتكون المكثفة من صفيحتين ناقلتين تفصل بينهما مادة عازلة للكهرباء ( الهواء ، خزف ، ميكا ، ورق ، شمع ، ... ) تدعى كل صفيحة لبوس المكثفة ويرمز لها بالرمز :

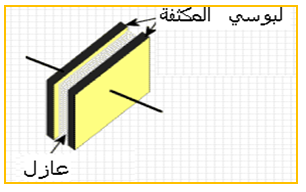
كمية الكهرباء
لما
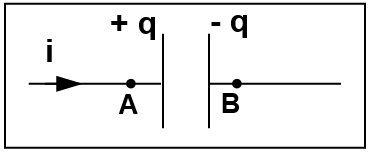
- نرمز للمقادير اللحظية ( المقادير التي تتغير بتغير الزمن ) بالرموز الصغيرة ، ونرمز لقيمها العظمى بالرموز الكبيرة.
- الشحنة عند اللبوسين متساوية القيمة و عليه .
- اذاكان فان شحنة المكثفةتتزايد ( شحن المكثفة ) .
- اذاكان (مرور التيار في الاتجاه المعاكس ) فان شحنة المكثفةتتناقص (تفريغ المكثفة ) .
العلاقة
وجد تجريبيا أن كمية الكهرباء
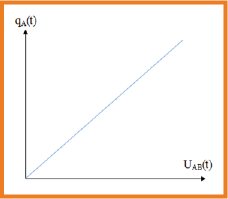
* الفاراد وحدة كبيرة جدا أمام سعات المكثفات المستعملة ولهذا تقدر في الغالب بأجزاء الفاراد وهي :
- الميكروفاراد () :
- النانوفاراد () :
- البيكو فاراد () :

مكثفة لبوساها مستويان متوازيان البعد بينهما

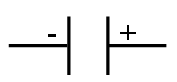
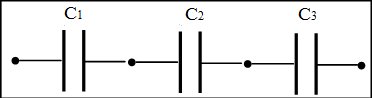
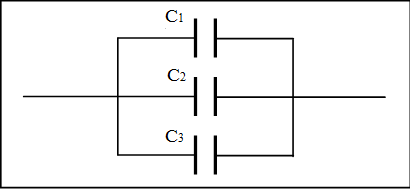
ماذا يحدث للمكثفة عندما توصل في دارة كهربائية ؟
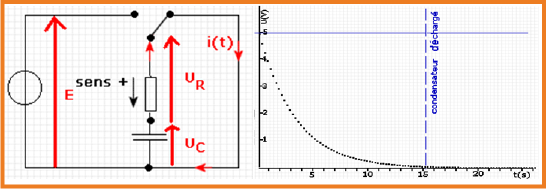
نربط على التسلسل مولد حقيقي قوته المحركة الكهربائية
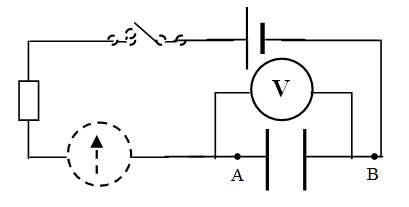
الشكل
عند غلق القاطعة سجل ملاحظتك.
نلاحظ مرور التيار لفترة قصيرة ثم ينعدم عندما يصل التوتر بين طرفي المكثفة إلى نفس قيمة التوتر
التفسير:
يعمل المولد على تحريك الإلكترونات من اللبوس
المكثفة شحنت.
بعد نهاية عملية الشحن إفتح القاطعة و اعزل المولد . بعد ذلك أغلق القاطعة . انظر الشكل
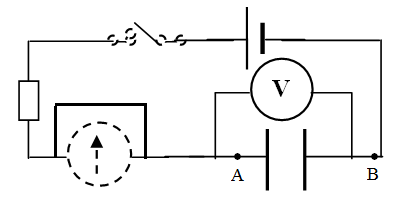
الشكل
سجل ملاحظتك حول التوتر بين طرفي المكثفة عند نهاية الشحن.
نلاحظ مرور التيار لفترة قصيرة في الإتجاه المعاكس ثم ينعدم ، تتوقف هذه الحركة عندما ينعدم التوتر بين طرفي المكثفة.
التفسير:
تعود الإلكترونات إلى اللبوس
المكثفة أفرغت.
تكون المكثفة غير مشحونة
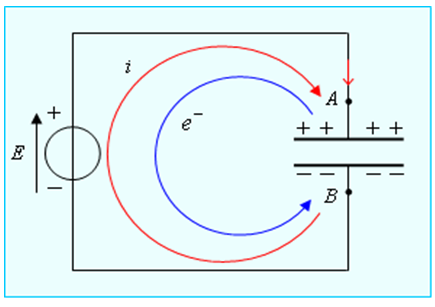
أما أثناء التفريغ، يزول تدريجيا الاختلال في التوازن الكهربائي إلى غاية الوصول إلى التوازن الابتدائي
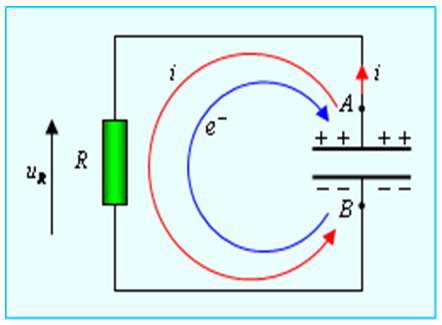
تخزن المكثفة أثناء شحنها كمية من الكهرباء و تعيدها أثناء التفريغ.
لدينا :
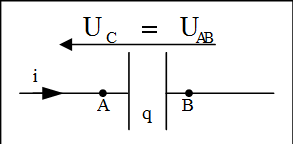
عند شحن المكثفة تخزن هذه الأخيرة كمية من الكهرباء و ويكون تطور فرق الكمون تدريجي و ليس تلقائي ليصل إلى قيمة ثابتة.
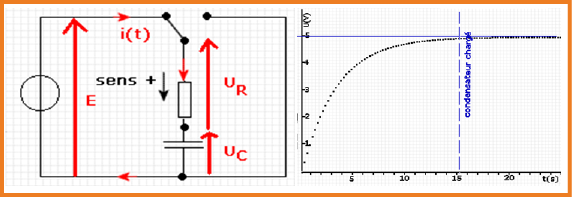
عند تفريغ مكثفة تعيد كمية الكهرباء ( تقدم للدارة شحنة ) ويكون تطور فرق الكمون تدريجي و ليس تلقائي ليصل إلى قيمة معدومة.
نسمي الجداء
ثابت الزمن
التحليل البعدي ثابت الزمن
لدينا :
من أجل مقاومة، يكون لدينا
نعوض كل هذا فنجد :
منه الجداء
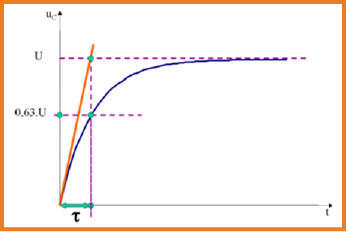
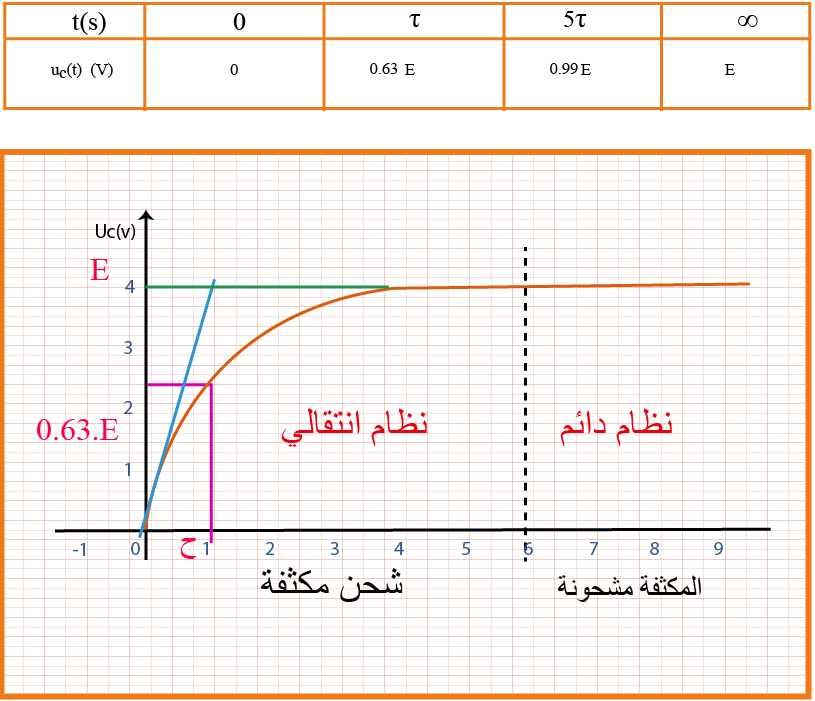
ثابت الزمن عبارة عن الزمن اللازم لكي يتم شحن أو تفريغ المكثفة بنسبة %63
يزداد ثابت الزمن
يزداد ثابت الزمن
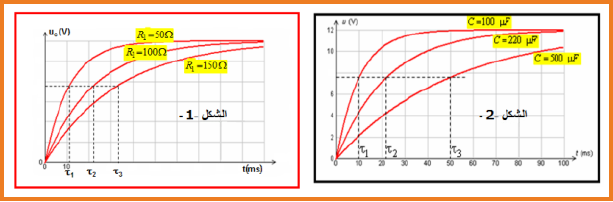
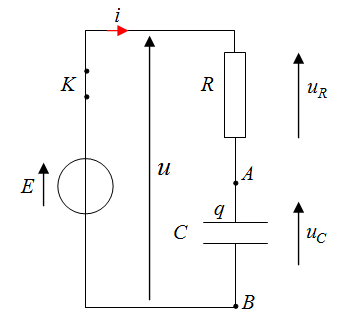
البيانات الملاحظة على راسم الإهتزاز المهبطي تبين أن
قانون جمع التوترات :
قانون أوم :
العلاقة شحنة – تيار :
العلاقة شحنة – توتر :
المعادلة الزمنية ( حل المعادلة التفاضلية ) :
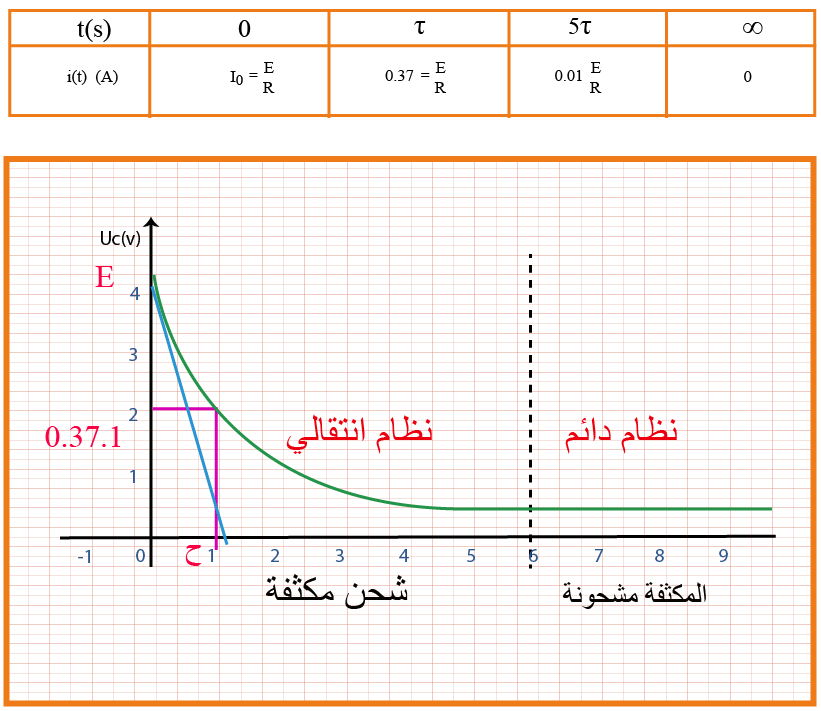
المعادلة الزمنية لشدة التيار المار في الدارة : عمليا شدة التيار خلال عملية الشحن تتناقص :
حيث أن :
بالاشتقاق نجد :
ومنه يكون :
البيانات الملاحظة على راسم الإهتزاز المهبطي تبين أن
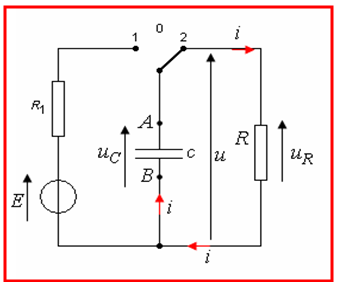
قانون جمع التوترات :
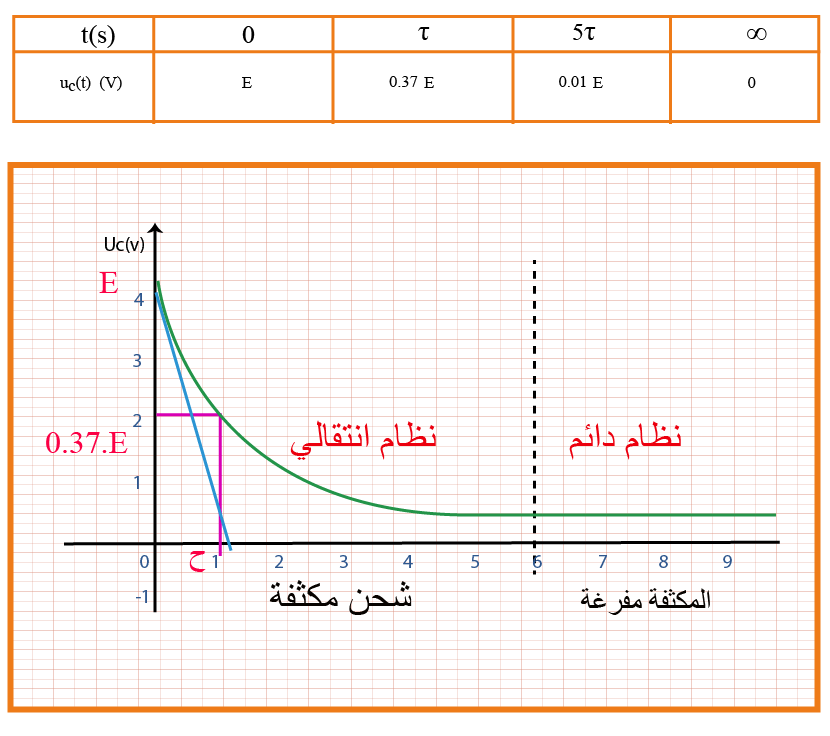
المعادلة الزمنية لشدة التيار المار في الدارة : شدة التيار خلال عملية التفريغ تتناقص حتى تنعدم لكن في الاتجاه المعاكس (السالب )
بالاشتقاق نجد
ومنه يكون :
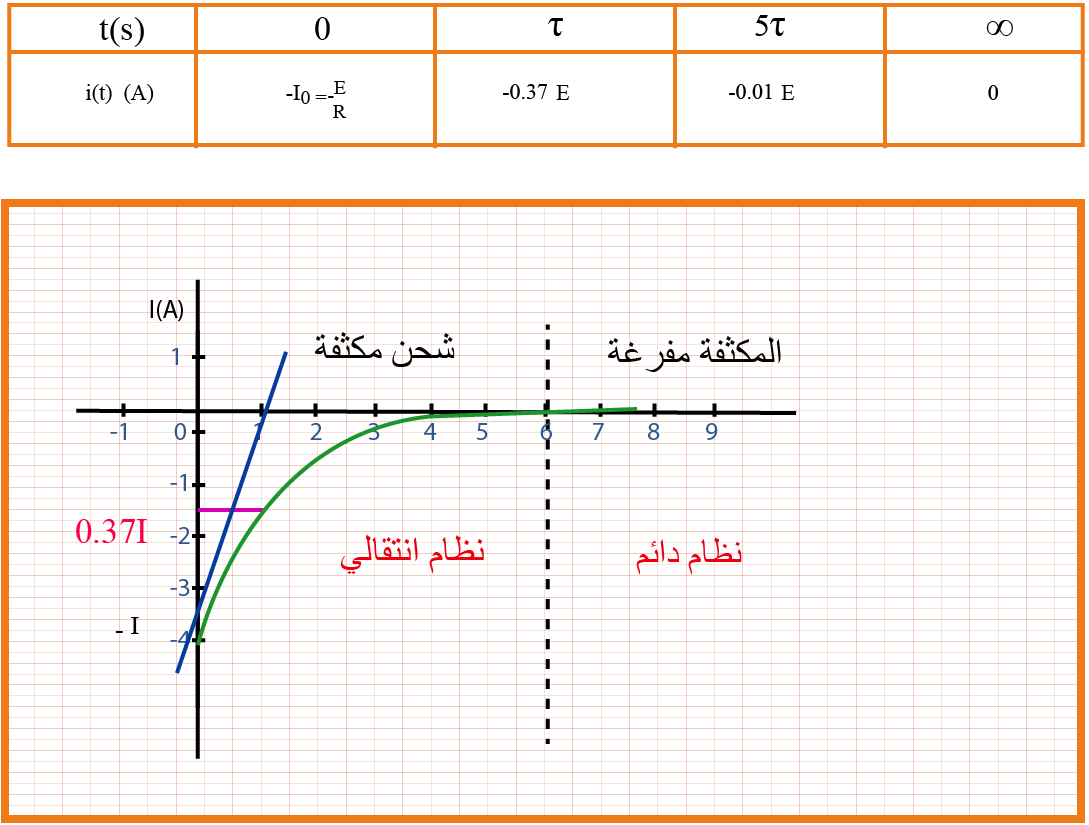
ان تطور التوتر بين طرفي المقاومة من تطور شدة التيار الكهربائي المار في الدارة و عليه :
حسب قانون التوترات:
نشتق طرفي المعادلة
لدينا :
نعوض
معادلة تفاضلية من الدرجة الأولى حلها من الشكل:
طريقة ثانية :
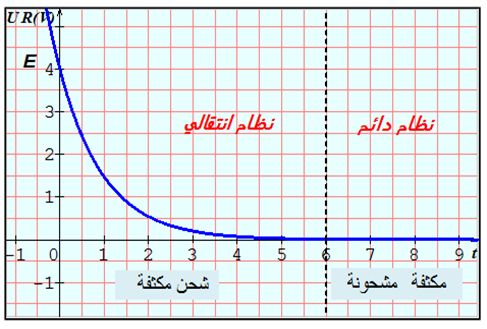
نفس الطريقة نجد :
معادلة تفاضلية من الدرجة الأولى حلها من الشكل :
طريقة ثانية :

ان تطور كمية الكهرباء ( الشحنة عند لبوسي المكثفة ) من تطور التوتر بين طرفي المكثفة
لدينا :
ومنه :
معادلة تفاضلية من الدرجة الأولى حلها من الشكل :
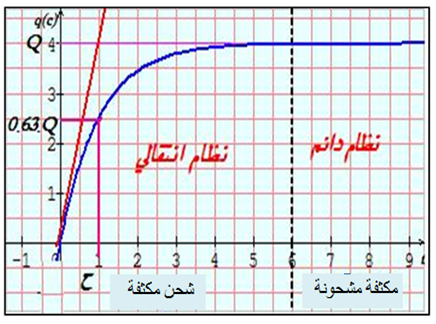
لدينا :
ومنه :
معادلة تفاضلية من الدرجة الأولى حلها من الشكل :
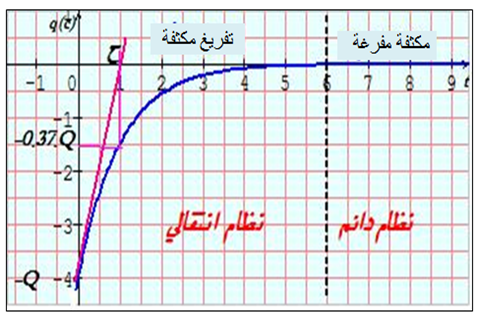
الطاقة المخزنة في مكثفة :
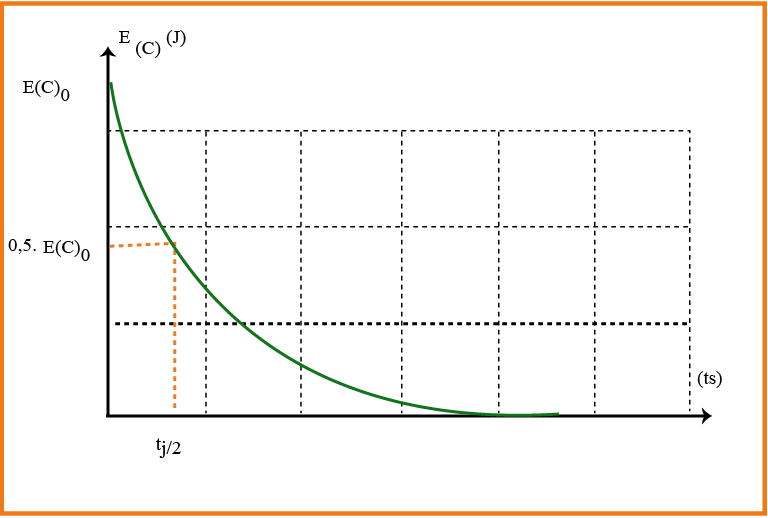
عبارة الطاقة المخزنة في المكثفة خلال التفريغ :
عند
فعند
بالتساوي نجد :
بأخذ لوغاريتم الطرفين نجد :
ومنه :
تتكون الوشيعة من سلك ناقل طويل جدا من النحاس معزول بطبقة من الورنيش ملفوف بشكل حلقات و تمتاز بذاتية
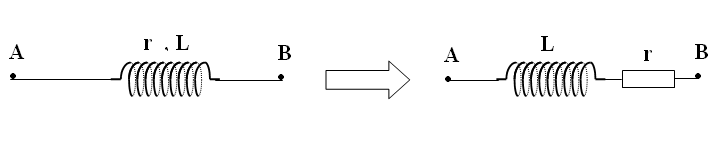
ملاحظة : اذا كانت الوشيعة صافية أو صرفة ( ) فتمثل كما يلي :
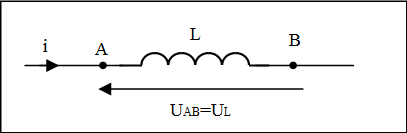
ملاحظة : اذا كانت الوشيعة صافية أو صرفة
ملاحظة :
- حالة تيار ثابت الشدة : الوشيعة تتصرف كناقل اومي :
- حالة وشيعة صرفة :
عندما نحقق الدارة الكهربائية الموضحة في الشكل فإنه :
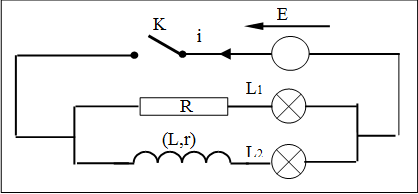
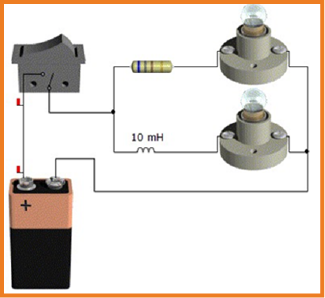
الملاحظة : توهج
ان الوشيعة تمانع التغير المفاجئ في شدة التيار، فتتحرض ذاتيا وينتج عن ذلك تيار متحرض معاكس لتيار المولد أي أن التيار المار في الدارة هو محصلة تيارين .
الملاحظة : ينطفئ
إن الوشيعة تخزن الطاقة الكهربائية.
للوشيعة تأثيرين :
- تأثير مقاومي ، وهو ناتج عن السلك الطويل المكون للوشيعة.
- تأثير تحريضي ، راجع لتغير شدة التيار المار في الدارة.
تمانع الوشيعة لوقت قصير تغير التيار في الدارة (نظام انتقالي)
تتصرف الوشيعة كناقل أومي عندما يجتازها تيار ثابت الشدة (نظام دائم).
نحقق الدارة الكهربائية الموضحة بالشكل نوصل راسم اهتزاز مهبطي مزود بذاكرة بين الوشيعة والناقل الأومي ( يستعمل راسم الاهتزاز المهبطي المزود بذاكرة لتسجيل التوتر اللحظي في الظواهر الكهربائية السريعة التي لا تستطيع العين المجردة مجاراتها ).
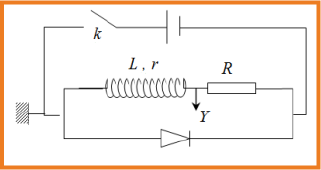
نميز حالتين :
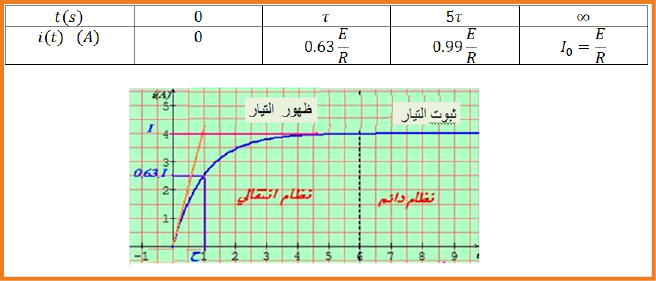
- عند غلق القاطعة يظهر المنحنى . شدة التيار تتزايد ببطئ الى ان تثبت عند قيمة عظمى.
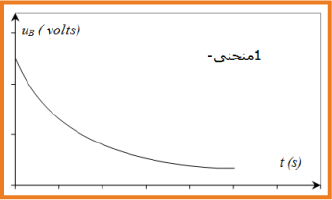
- عند فتح القاطعة يظهر المنحنى . شدة التيار تتزايد ببطئ الى ان تثبت عند قيمة عظمى
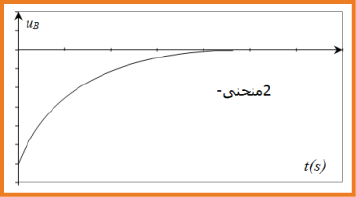
يعطى بالعبارة :
التحليل البعدي لعبارة ثابت الزمن :
لدينا :
ومنه :
أي أن:
لدينا أيضا :
ومنه الثابت
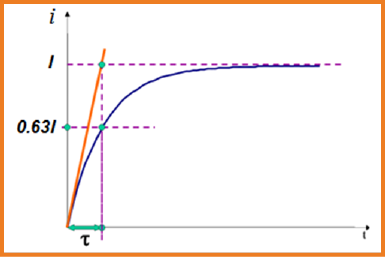
ثابت الزمن
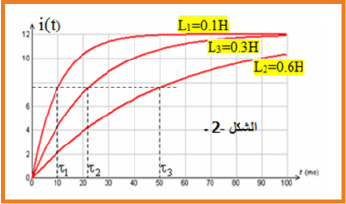
يزداد ثابت الزمن
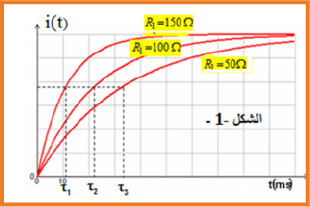
يزداد ثابت الزمن
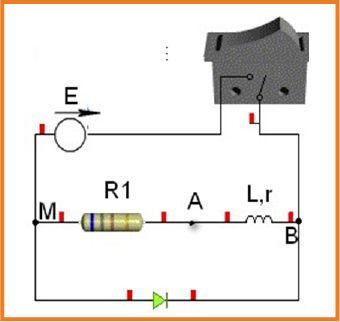
عند غلق القاطعة يتزايد مرور التيار في الدارة ببطئ.
حسب قانون جمع التوترات :
نضع
حيث أن
نستطيع أن نكتب:
معادلة تفاضلية من الدرجة الأولى حلها من الشكل :
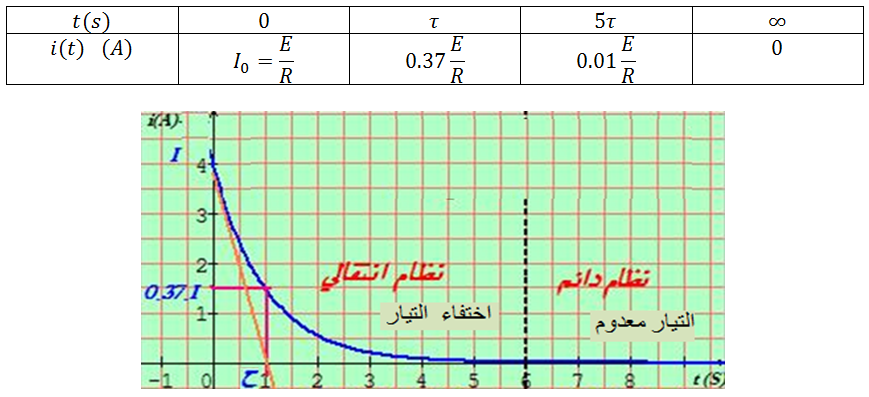
عند فتح القاطعة يتناقص مرور شدة التيار ببطئ
حسب قانون جمع التوترات :
نضع
حيث أن
معادلة تفاضلية من الدرجة الأولى حلها من الشكل:
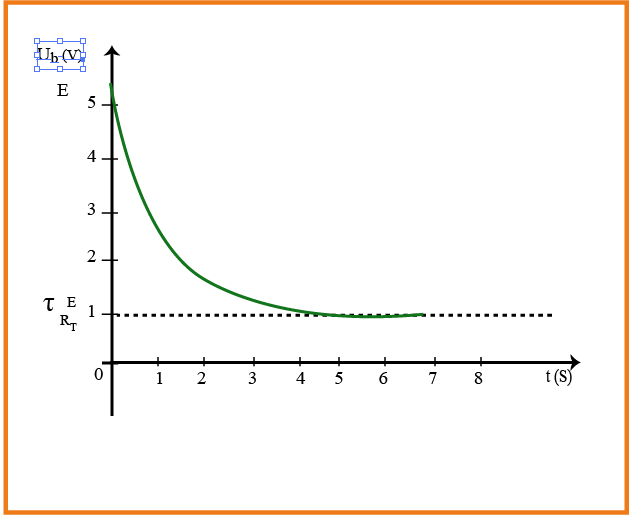
لدينا :
بالاشتقاق نجد:
بالتعويض:
ومنه :
اي:
- في حالة وشيعة صافية : نضع في عبارة الأخيرة فنجد :
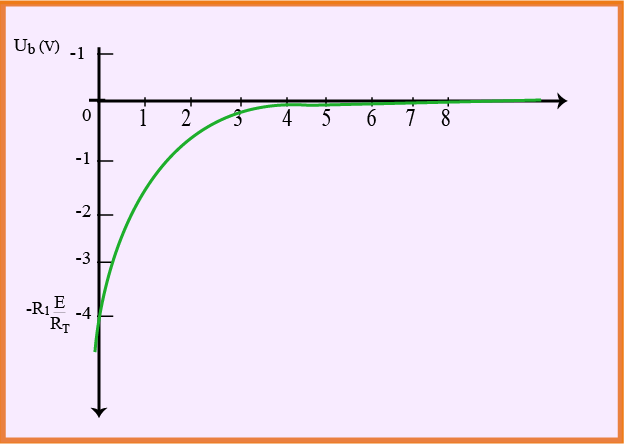
لدينا :
بالاشتقاق نجد :
بالتعويض :
- في حالة وشيعة صافية : نضع في عبارةالأخيرة فنجد :
لدينا :
حسب قانون جمع التوترات :
بتعويض عن عبارة
معادلة تفاضلية من الدرجة الأولى حلها من الشكل
يمكن التأكد من الحل بطريقة بسيطة :
لدينا :
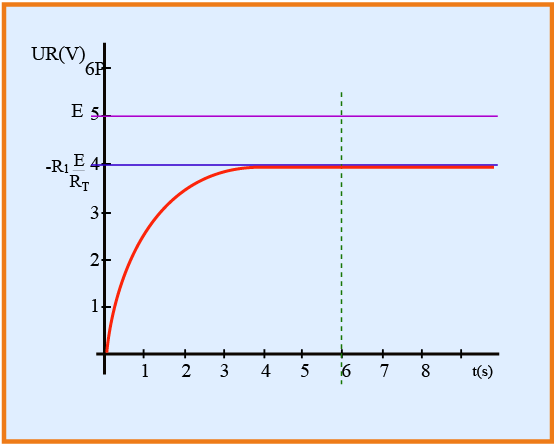
لدينا :
بالتعويض عبارة
معادلة تفاضلية من الدرجة الأولى حلها من الشكل :
يمكن التأكد من الحل بطريقة بسيطة :
لدينا :
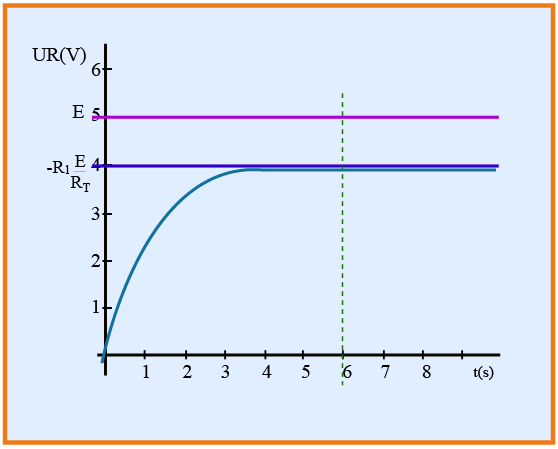
تخزن الوشيعة طاقة كهرومغناطيسية بفعل ذاتيتها
زمن تناقص طاقة الوشيعة إلى النصف
- إختبارات
- 20
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- Anis Abdellaoui
- 241 نقطة
-

- adidi zitouni
- 200 نقطة
-

- ZINO OUNISSI
- 200 نقطة
-

- oussama hoho
- 190 نقطة
-

- admin imad edinne
- 183 نقطة
-

- nadjla selma labri
- 183 نقطة
-
- Prin Cesse *_*
- 183 نقطة
-

- daser hamid
- 183 نقطة
-

- ahmed attou
- 177 نقطة
-

- Mohamed nazim Sahraoui
- 177 نقطة
-










