التطورات المهتزة
الجملة الميكانكية المهتزة : هى كل جملة تقوم بحركة ذهاب واياب على جانبى وضع توازنها المستقر مثل الارجوحة .رقاص ساعة الحائط .النواس المرن .النواس الثقلى .... اذا كان زمن الذهاب والا ياب او مايسمى زمن حركة او زمن اهتزازة يبقى ثابت نقول ان النظام دوري ودوره الذاتي
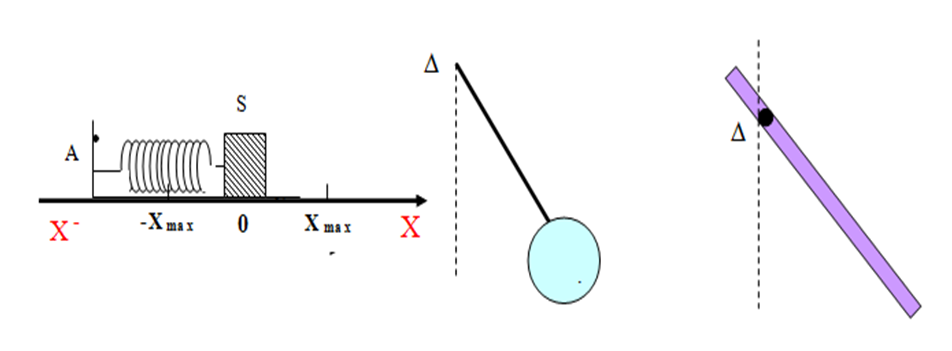
ونسمي اقصى فاصلة يصل اليها الجسم المهتز على جانبى وضع التوازن المستقر بالسعة العظمى ويرمزلها
وتنقسم الاهتزازات الميكانكية الى الاقسام التالية
نقول عن جملة انها تهتز اهتزازات حرة عندما تهتز من تلقاء نفسها دون ان تتلقى طاقة من الوسط الخارجى وتنقسم هذه الاهتزازات بدورها الى
وتبقى طاقتها ثابته بمرور الزمن اى ان سعته العظمى لاتتغيرعندما نسحب الكتلة عن وضع توازنها ثم نحررها تتغير فاصلتها بين قيمتين حديتين
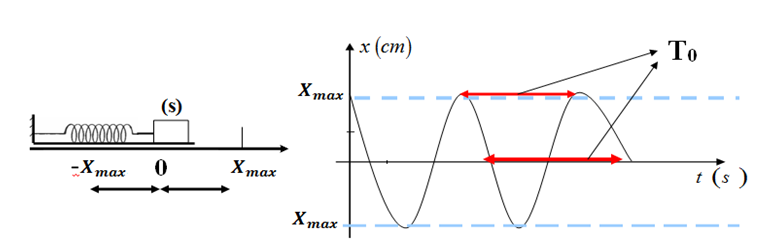
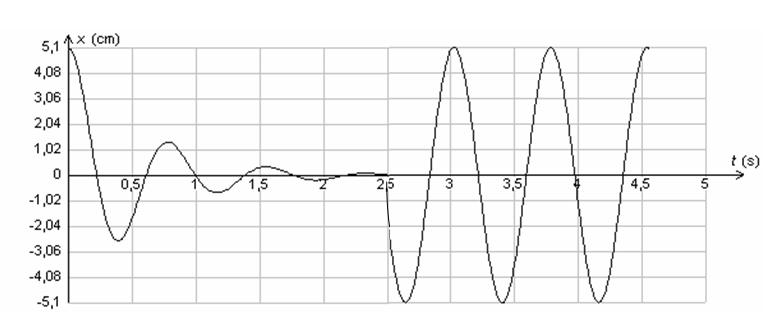
هى الاهتزازات الحرة التى تفقد فيها الجملة جزءا من طاقتها بفعل الاحتكاك وبالتالى تتناقص سعتها تدريجيا حتى تتوقف الجملة عن الاهتزاز ونميز حالتين الاحتكاكات ضعيفة تناقص الطاقة يكون تدريجى والنظام شبه دورى ودوره
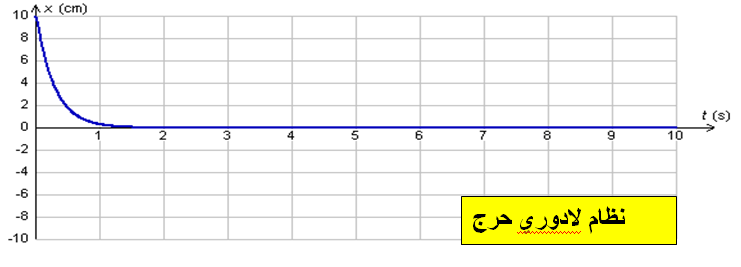
حيث كل مازاد الاحتكاك زاد التخامد اذاكانت الاحتكاكات فعالة جدا لا تهتز الجمالة والنظام لا دوري حرج
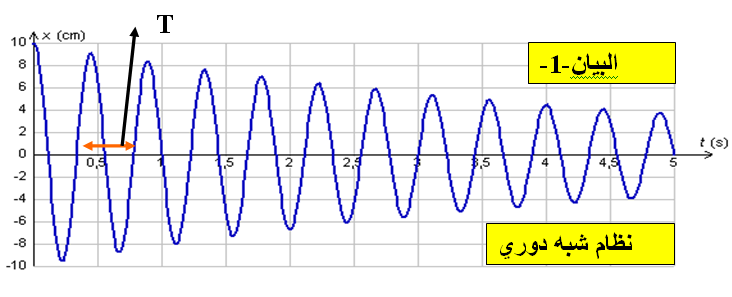
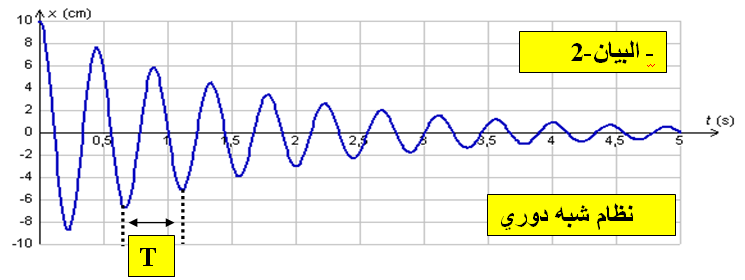
نقول عن جملة ان اهتزازه حر مغذى عندما تهتز دون مؤثر خارجى ونعوض باستمرار كل الطاقة و الضائعة بتجهيز مناسب حسب الجملة وبالتالى تبقى سعة الاهتزازة ثابتة
نقول عن جملة ما فى شروط معينة انها تتعرض لاهتزازات قسرية عندما يفرض عامل خارجى ( المحرض) دور اهتزازاته على هذه الجملة ( التجاوب)
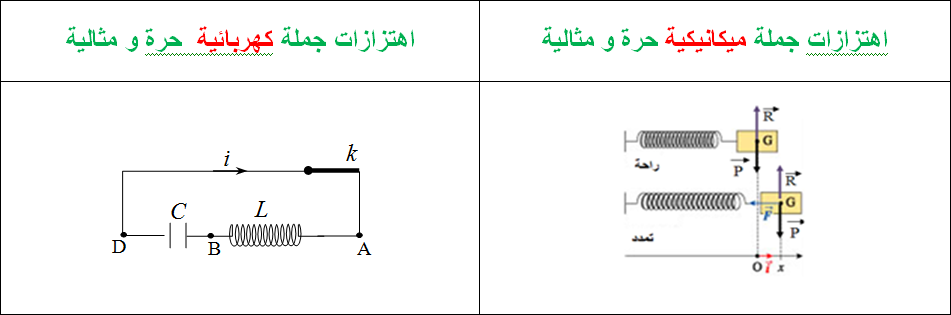
وهو عبارة عن نابض مرن مهمل الكتلة ذو حلقات متلاصقة احد طرفيه مثبت والطرف الاخر يحمل كتلة نقطية حسب الشكل فان الكتلة تهتز اهتزاز حر غير متخامد دورى
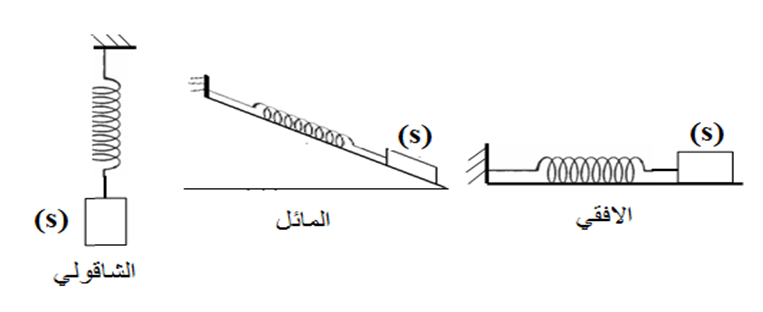
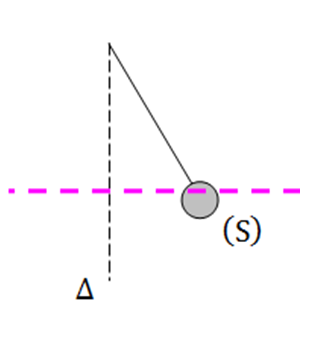
هو جسم يهتز حول محور دوران افقى ثابت لا يمر من مركز عطالته
فى حالة كرة صغيرة ابعادها مهملة ومعلقة فى خيط مهملالكتلة وعديم التمدد او ساق مهملة الكتلة يسمى نواس ثقلى بسيط او اختصارا نواس بسيط
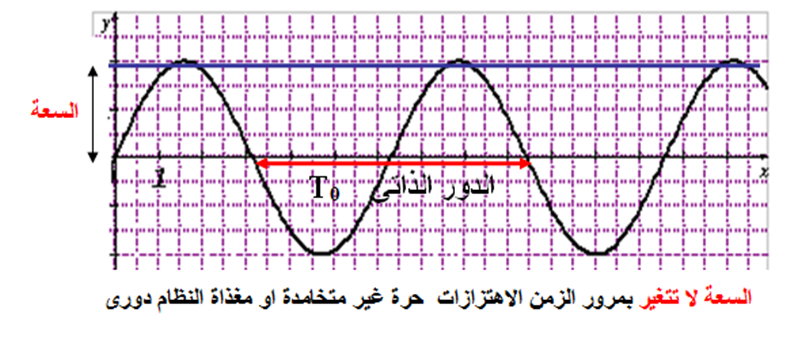
اذا كانت الجملة تهتز اهتزاز حر غير متخامد او اهتزاز حر مغذى فان الحركة تكرر نفسها خلال فترات زمنية متتالية ومتساوية وكل فترة تسمى بالدور الذاتى للجملة ونرمز
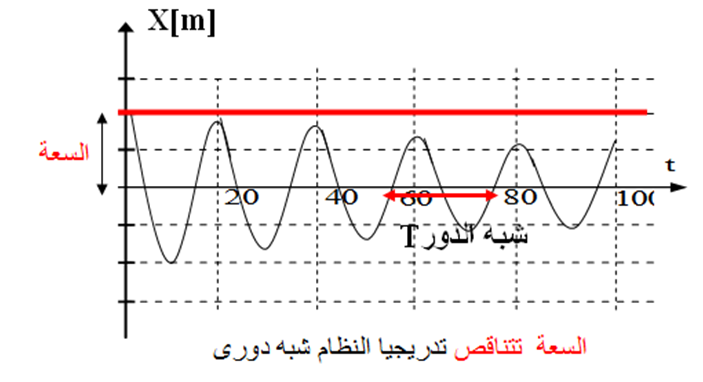
عندما تكون هناك احتكاكات ضعيفة او غير فعالة فان السعة تتناقص تدريجيا الى ان تنعدم ونقول ان النظام شبه دورى ودوره
نزيح الجسم ثم نتركه لحاله دون سرعة ابتدائية عند
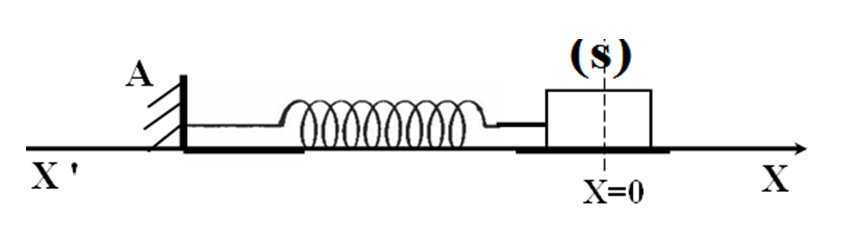
يتحرك الجسم
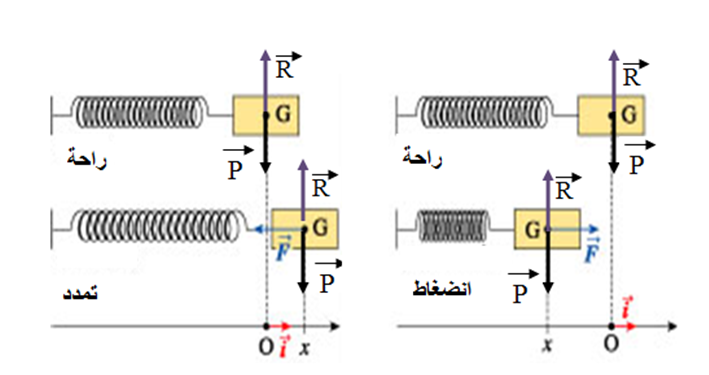
- الحركة اهتزازية دورية
- والجملة لا تتلقى طاقة من الوسط الخارجي فهي جملة مهتزة حرة .
بتطبيق القانون الثانى لنيوتن
باسقاط العلاقة على المحور
بالمطابقة نجد ان
و عليه
حل المعادلة هو
و البياني هو
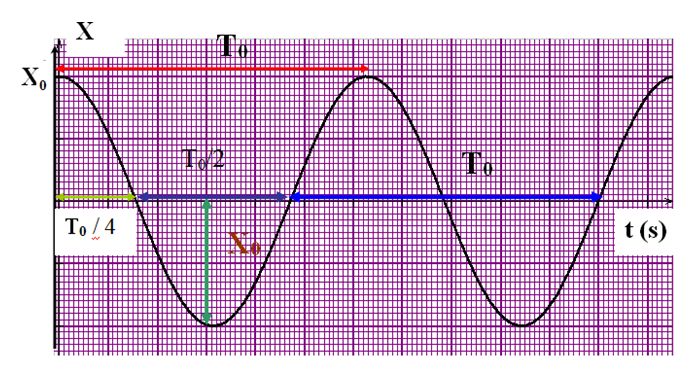
حيث
: سعة الحركة (أكبر قيمة للفاصلة) او المطال الاعظمى
: الصفحة الابتدائية للحركة وتتعلق قيمتها بالشروط الابتدائية للحركة.
تحدد بالشروط الابتدائية مثلا في الشكل
و تصبح المعادلة
دورها الزمن اللازم للقيام بدورة ( ذهاب و اياب )
عبارة السرعة
بيانها :
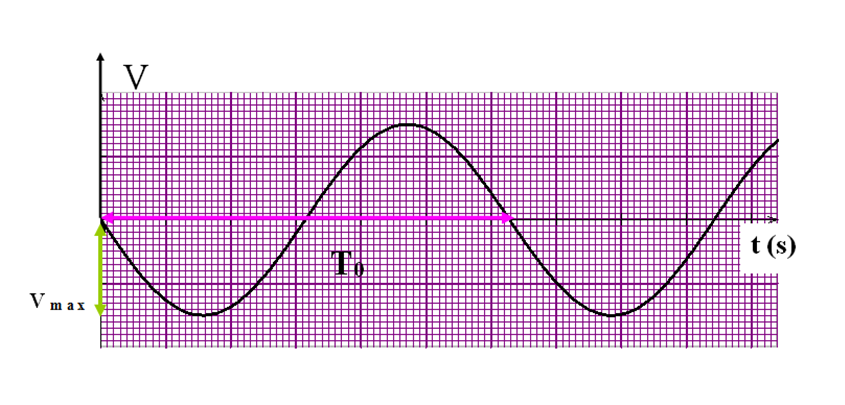
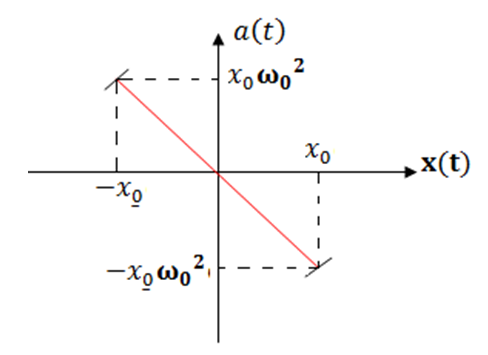
عبارة التسارع :
بيانها :
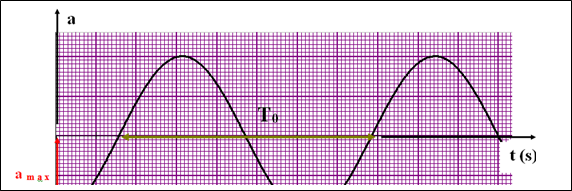
نختار الجملة هى الارض- نابض ونختار النابض فى وضعية الراحة المستوى المرجعى للطاقة الكامنة المرونية والمستوى الافقى الذى يشمل المحور والنابض هو مستوى مرجعى للطاقة الكامنة الثقالية
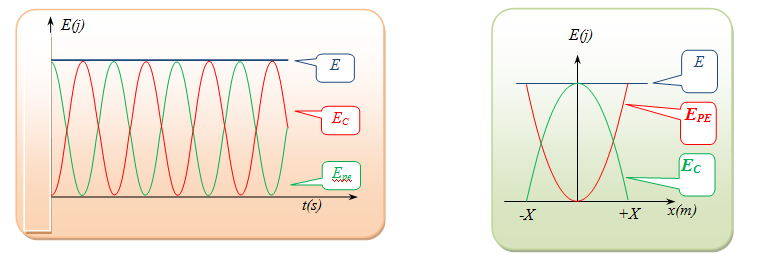
(حالة غياب الاحتكاكات) طاقة الجملة: ( نابض ، جسم)
طاقة الجملة = الطاقة الحركية + الطاقة الكامنة
اذن:
إثبات أن طاقة الجملة ثابتة في كل لحظة:
مع
بالتعويض نجد:
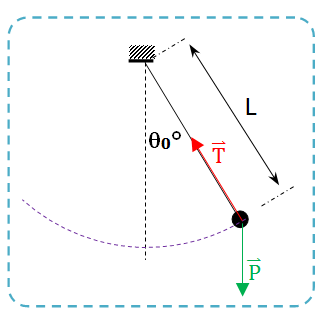
هو كل جسم صلب بامكانه الاهتزاز حول محور ثابت و أفقي لا يمر من مركز عطالته مثل: الأرجوحة - رقاص ساعة حائطية
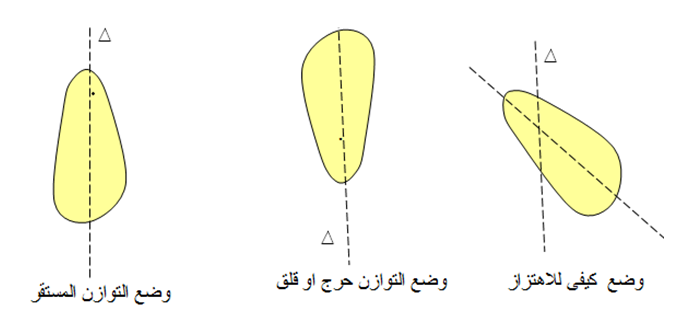
يكون النواس الثقلي في حالة توازن عندما يكون مركز عطالته واقعا على نفس الشاقول مع نقطة تعليقه فاذا كان اسفل منها يكون في توازن مستقر واذا كان أعلى منها يكون في حالة توازن قلق ( مضطرب – غير مستقر )
- حالة الحركة دون احتكاكات : تكون الاهتزازات دورية غير متخامدة
- حالة الحركة بالاحتكاك : نميز حالتين
- احتكاكات مائعة تكون الحركة متخامدة بنظام شبه دوري أسي
- احتكاكات صلبة تكون الاهتزازات متخامدة بنظام شبه دوري خطي
نزيح كرة النواس بزاوية إزاحة ابتدائية
- توازن النواس: يكون النواس في حالة توازن عندما يكون شاقوليا
- حركة النواس: عند الحركة نلاحظ أن النواس يقوم بحركة دورية
- يزداد دوره ببعد مركز عطالته عن محور الدوران ( طول النواس
- يقل دوره بزيادة الإرتفاع عن الأرض ( نقصان الجاذبية
- لا يتأثر دوره بالكتلة المعلقة
يتم الوصول إلى عبارة الدور الذاتي من أجل الاهتزازات صغيرة السعة
من أجل السعات الكبيرة يعطى الدور بالعبارة التالية :
حيث
: الدور الذاتي من اهتزازات صغيرة السعة
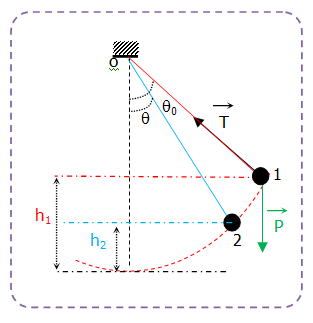
إن الجملة ( كتلة + أرض ) تملك طاقة حركية وكامنة ثقلية
نعتبر المستوى المرجعي لقياس الطاقة الكامنة الثقلية المستوي الأفقي المار بوضع التوازن
من معادلة انحفاظ الطاقة:
حيث
أي أن
باشتقاق المعادلة من الطرفين نحصل على:
من أجل الزوايا الصغيرة يكون
فإن
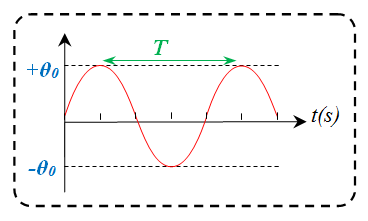
حلها جيبيا من الشكل
دورها الذاتي:
 (
(
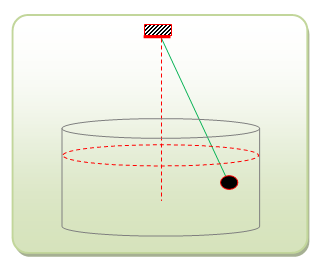
نجعل النواس داخل حوض به ماء و نراقب حركته بعد ازاحته عن وضع توازنه تكون سعة النواس متناقصة تدريجيا حتى تنعدم نتيجة لزوجة الماء الضعيفة لذا تكون الاهتزازات شبه دورية متخامدة نعيد نفس التجربة لكن باستبدال الماء بالزيت نلاحظ أن النواس لا يهتز نتيجة اللزوجة المرتفعة للزيت وتكون النظام لا دوري حرج
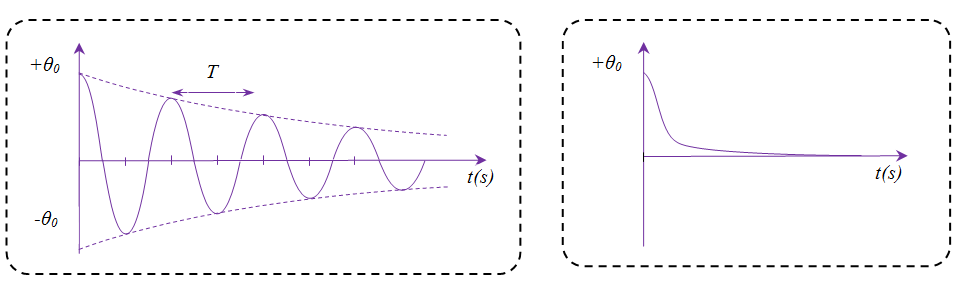
يزداد التخامد كلما زادت فعالية الاحتكاكات حيث:
من أجل الاحتكاكات الضعيفة يكون الاهتزاز شبه دوري متخامد الشكل
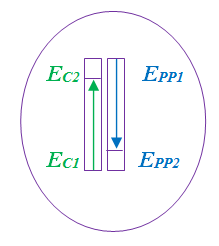
ندعو جملة كهربائية مهتزة كل دارة تحتوي على وشيعة ، مكثفة مشحونة ومقاومة
نحقق دارة كهربائية كما بالشكل المقابل:
نعتبر مقاومة الدارة
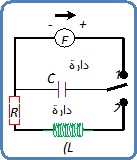
بواسطة الدارة
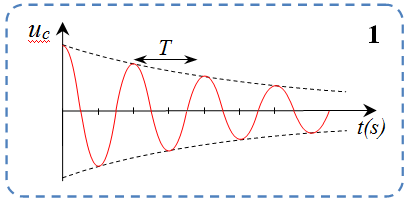
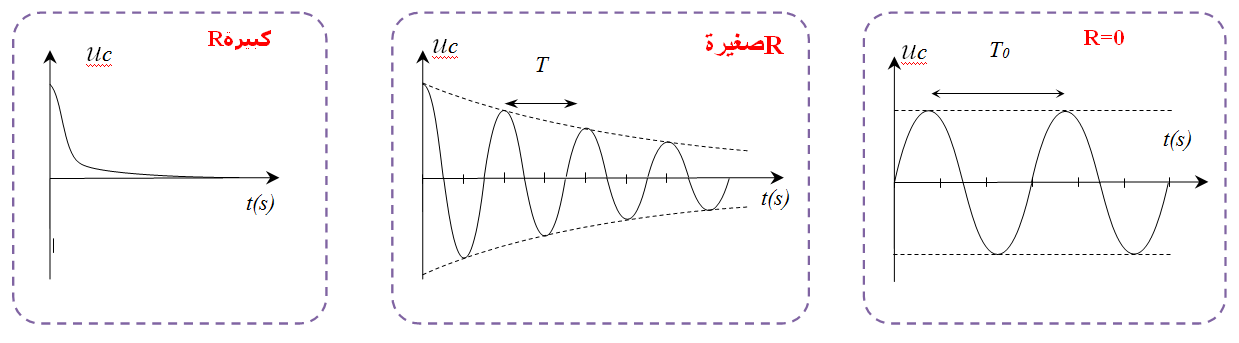
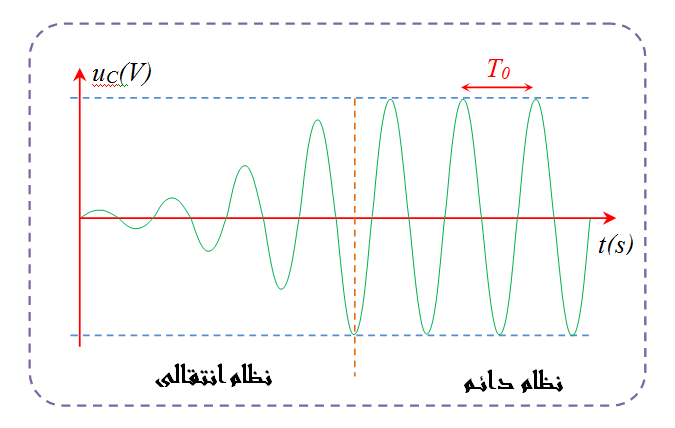
إن البيان يدل على أن التوتر بين طرفي المكثفة متخامد
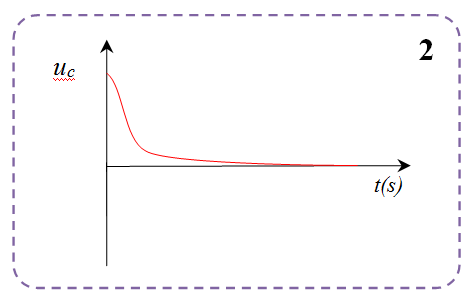
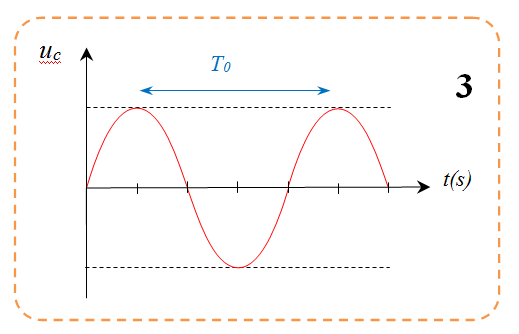
عند جعل مقاومة الدارة معدومة
باستخدام قانون جمع التوترات لدينا
بالتعويض نجد
بالقسمة على
وهي معادلة تفاضلية من الرتبة الثانية حلها منحناها البياني الشكل
- من أجل
- من أجل
- من أجل
من الشكل
حلها جيبيا
نبضها الذاتي
نقول عن النظام الكهربائي في هذه الحالة أنه دوري غير متخامد .
إن طاقة الدارة في أي لحظة هي طاقة الوشيعة والمكثفة
من المعادلة التفاضلية بدلالة
من
التغير في الطاقة غير معدوم مما يدل على أنه يوجد ضياع في الطاقة ( فعل جول )
سبب هذا الضياع هو وجود المقاومة
ومن اجل دارة لا تحتوي على مقاومة فإن
ويكون النظام غير متخامد دوري دوره الذاتي
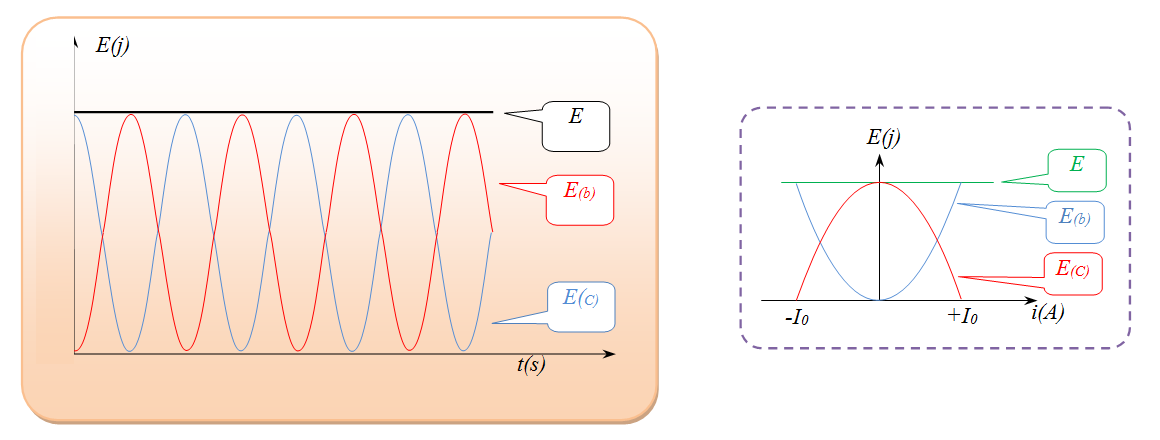
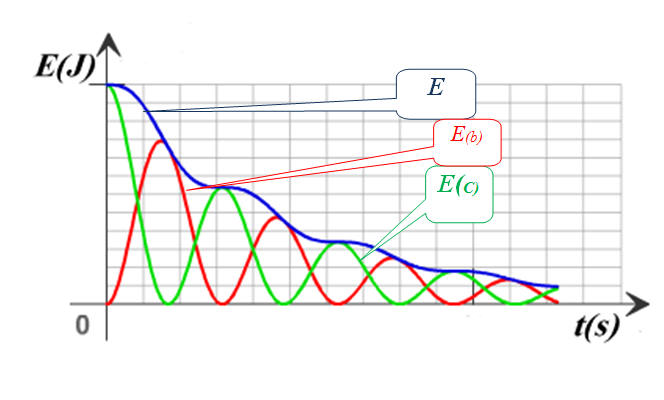
إن المسؤول عن تخامد الاهتزازات هو المقاومة ولذلك يمكن تغذية الدارة بتوصيلها بجهاز( مضخم تطبيقي
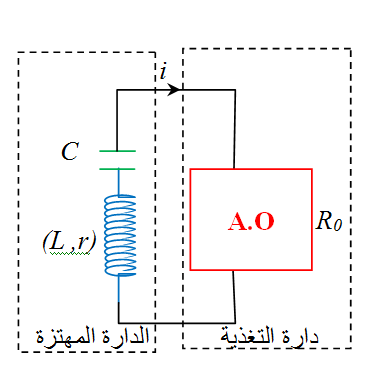
حيث يكون قانون التوترات كالتالي:
فيتحول بذلك النظام من اهتزازي متخامد إلى نظام اهتزازي مغذى غير متخامد.
نقول عن جملة أنها تهتز باهتزازات قسرية إذا فرض عليها اهتزازات من عامل خارجي حيث يزودها بالطاقة دوريا ولذا يسمى العامل الخارجي محرض والجملة مجاوب وعندما يكون تواتر المحرض متوافق مع التجاوب نقول أنه حدث تجاوب بينهما فتهتز الجملة عندئذ بأكبر سعة ممكنة
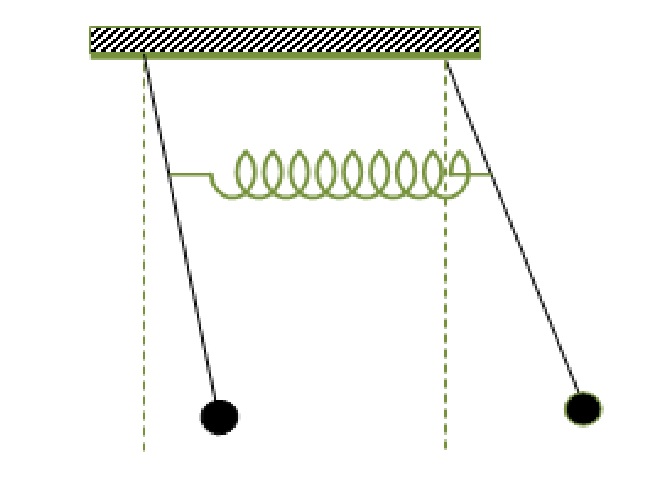
نحقق التركيب التالي: نعتبر النواس
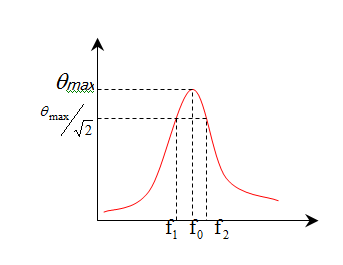
نغير طول النواس المحرض من أجل تغيير دوره فنلاحظ أن سعة الأهتزاز في النواس المجاوب تزداد كذلك وتصل إلى قيمتها الأعظمية من أجل
تقل سعة إهتزاز المجاوب
النواس المحرض وسعة إهتزاز المجاوب كما بالشكل:
تكون سعة الاهتزاز مقبولة من أجل
تحدث الاهتزازات القسرية الكهربائية عندما نفرض على الدارة
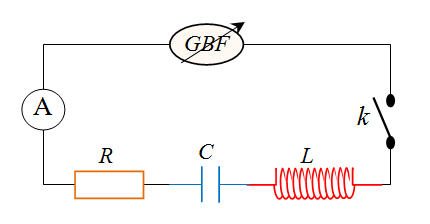
نوصل الدارة بمقياس أمبير لقياس شدة التيار وكذلك يستعمل مدخلي راسم اهتزاز مهبطي
نحصل على المنحنى المقابل
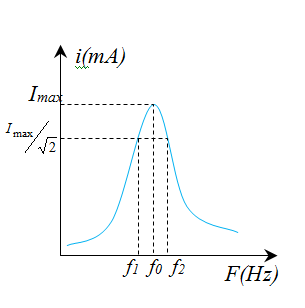
تكون شدة التيار معتبرا من أجل
معامل الجودة: هو مقدار يعبر عن حالة التجاوب ويعطى بالعلاقة
نعيد التجربة السابقة من اجل قيمة أكبر للمقاومة
نحصل على المنحنى المقابل:
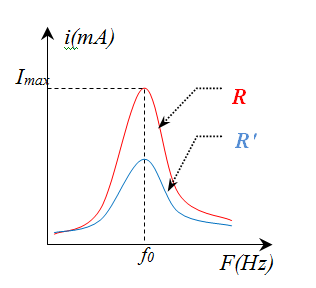
من أجل المقاومة الصغيرة
من أجل المقاومة الكبيرة
هي العرقلة التي تبديها الدارة للتيار الكهربائي المار فيها يرمز لها بالرمز
تأثير
نعيد الدارة السابقة ونغير كل مرة أحد العناصر
نلاحظ ان هذه التغيرات تكون وفق المنحنيات التالية:
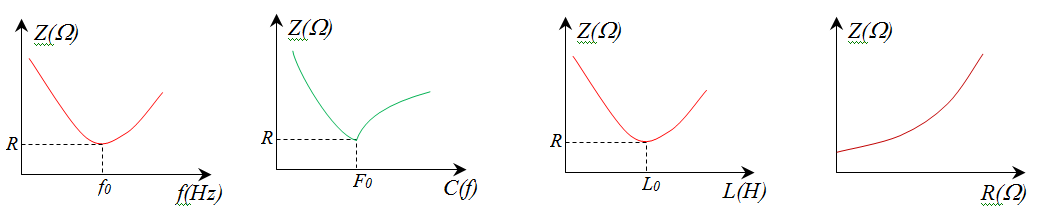
- تزداد ممانعة الدارة بزيادة المقاومة
- تتناقص قيمة الممانعة بزيادة الذاتية إلى أن تصل إلى قيمة حدية صغرى
- تتناقص قيمة الممانعة بزيادة السعة إلى أن تصل إلى قيمة حدية صغرى
ثم يزداد بعد ذلك

- إختبارات
- 20
- الأجوبة الصحيحة
- False
- الأجوبة الخاطئة
- False
- مجموع النقاط
- False
المراتب الخمس الأولى في Quiz
- صلاح بشير الشريف
- 178 نقطة
-

- طالب مترشح
- 173 نقطة
-

- Mohamed BENFERHAT
- 154 نقطة
-

- imane dadou
- 145 نقطة
-

- Sifodil Alaa
- 144 نقطة
-
- safaa messaoud
- 140 نقطة
-

- Wafaa Tabet
- 131 نقطة
-

- Guerr AMM
- 117 نقطة
-
- Lotfi Fardeheb
- 108 نقطة
-
- amjed deham
- 98 نقطة
-










